题目内容
18.设an=1+2+3+…+n,bn=12+22+32+…+n2,观察下表:| n | 1 | 2 | 3 | 4 | 5 | … |
| an | 1 | 3 | 6 | 10 | 15 | … |
| bn | 1 | 5 | 14 | 30 | 55 | … |
分析 根据图示,可得$\frac{{a}_{1}}{{b}_{1}}=\frac{1}{1}=\frac{3}{2×1+1}$,$\frac{{a}_{2}}{{b}_{2}}=\frac{3}{5}=\frac{3}{2×2+1}$,$\frac{{a}_{3}}{{b}_{3}}=\frac{6}{14}=\frac{3}{7}=\frac{3}{2×3+1}$,$\frac{{a}_{4}}{{b}_{4}}=\frac{10}{30}=\frac{3}{9}=\frac{3}{2×4+1}$,…,所以$\frac{{a}_{n}}{{b}_{n}}$与n的关系的等式为:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$,据此解答即可.
解答 解:∵$\frac{{a}_{1}}{{b}_{1}}=\frac{1}{1}=\frac{3}{2×1+1}$,
$\frac{{a}_{2}}{{b}_{2}}=\frac{3}{5}=\frac{3}{2×2+1}$,
$\frac{{a}_{3}}{{b}_{3}}=\frac{6}{14}=\frac{3}{7}=\frac{3}{2×3+1}$,
$\frac{{a}_{4}}{{b}_{4}}=\frac{10}{30}=\frac{3}{9}=\frac{3}{2×4+1}$,
…,
∴$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$,
即$\frac{{a}_{n}}{{b}_{n}}$与n的关系的等式:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$.
故答案为:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律.

| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
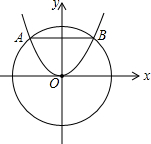 如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )
如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 4 |
| A. | 打开电视机,正在播放湛江新闻 | B. | 下雨后,天空出现彩虹 | ||
| C. | 随机掷一枚硬币,落地后正面朝上 | D. | 早晨的太阳从东方升起 |
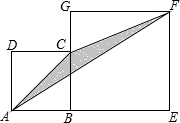 如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8.
如图,四边形ABCD和四边形BEFG均为正方形,且A、B、E三点共线,正方形ABCD的边长为4,则S△ACF的面积为8.