题目内容
13.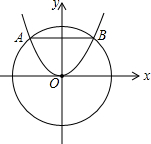 如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )
如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 4 |
分析 根据AB=4,求出BC的长,得到点B的横坐标,代入抛物线的解析式求出点B的纵坐标,得到OC的长,根据勾股定理求出OB的长,得到答案.
解答 解: 如图,连接OB,
如图,连接OB,
∵AB=4,
∴BC=2,
则点B的横坐标为2,
y=$\frac{1}{2}$x2=2,
∴点B的坐标为(2,2),
∴OC=2,
在Rt△OCB中,BC=2,OC=2,
由勾股定理得,OB=2$\sqrt{2}$,
故选:B.
点评 本题考查的是二次函数图象上点的坐标特征和勾股定理的应用,理解坐标与图形的关系、灵活运用数形结合思想是解题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.若代数式$\sqrt{x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-6 | B. | x>6 | C. | x≥6 | D. | x≤6 |
8.下列几项调查中,适合使用普查的是( )
| A. | 调查我区奶制品中蛋白质含量是否达到国家标准 | |
| B. | 调查我区6月1日这天嘉陵江水中氨氮含量是否超标 | |
| C. | 调查我校初三某班全体学生的视力状况 | |
| D. | 调查我区市民对消防安全知识的知晓情况 |
18.设an=1+2+3+…+n,bn=12+22+32+…+n2,观察下表:
写出$\frac{{a}_{n}}{{b}_{n}}$与n的关系的等式:$\frac{{a}_{n}}{{b}_{n}}$=$\frac{3}{2n+1}$.
| n | 1 | 2 | 3 | 4 | 5 | … |
| an | 1 | 3 | 6 | 10 | 15 | … |
| bn | 1 | 5 | 14 | 30 | 55 | … |
 如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.
如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上. 如图,Rt△ABC绕着点A顺时针旋转90°得到△AB′C′,若∠B=25°,∠C=90°.则∠BAC′的度数是25°.
如图,Rt△ABC绕着点A顺时针旋转90°得到△AB′C′,若∠B=25°,∠C=90°.则∠BAC′的度数是25°. 如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.
如图,在Rt△ABC中,已知:∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△DEF,则四边形MPQN的面积为$\frac{9}{4}$cm2.