题目内容
如图，在平面直角坐标系中，正方形OABC的顶点O为坐标原点，点B（0，6），反比例函数y=| k |
| x |
考点：反比例函数图象上点的坐标特征,正方形的性质
专题：
分析：过点C作CD⊥y轴于点D，故可得出BD=CD=
OB=3，故可得出C点坐标，进而得出结论．
| 1 |
| 2 |
解答：
解：过点C作CD⊥y轴于点D，
∵正方形OABC的顶点O为坐标原点，点B（0，6），
BD=CD=
OB=3，
∴C（3，3）．
∵反比例函数y=
的图象过点C，
∴k=3×3=9．
故答案为：9．
解：过点C作CD⊥y轴于点D，∵正方形OABC的顶点O为坐标原点，点B（0，6），
BD=CD=
| 1 |
| 2 |
∴C（3，3）．
∵反比例函数y=
| k |
| x |
∴k=3×3=9．
故答案为：9．
点评：本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
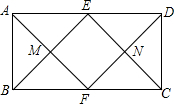如图，在矩形ABCD中，E，F分别是AD，BC中点，连接AF，BE，CE，DF分别交于点M，N，四边形EMFN是（ ）| A、正方形 | B、菱形 |
| C、矩形 | D、无法确定 |
下列说法错误的个数是（ ）
①无理数都是无限小数；
②
的平方根是±2；
③
=（
）2；
④与数轴上的点一一对应的数是实数．
①无理数都是无限小数；
②
| (-2)2 |
③
| a2 |
| a |
④与数轴上的点一一对应的数是实数．
| A、1个 | B、2个 | C、3个 | D、4个 |
如图是一个几何体的三视图，根据图纸标注的数据，求得这个几何体的侧面积是（ ）
| A、12π | B、15π |
| C、24π | D、30π |