题目内容
已知梯形ABCD中,AD∥BC,AD=1,BC=2,sinB=
,过点C在∠BCD的内部作射线交射线BA于点E,使得∠DCE=∠B.

(1)如图1,当ABCD为等腰梯形时,求AB的长;
(2)当点E与点A重合时(如图2),求AB的长;
(3)当△BCE为直角三角形时,求AB的长.
| 3 |
| 5 |

(1)如图1,当ABCD为等腰梯形时,求AB的长;
(2)当点E与点A重合时(如图2),求AB的长;
(3)当△BCE为直角三角形时,求AB的长.
考点:相似形综合题
专题:
分析:(1)作AM∥DC交BC于点M,AH⊥BC于点H,AD=1,BC=2,sinB=
,得到AM=AB,BH=HM=
,结合三角函数的定义可以求得AB的长.
(2))由AD∥BC得到∠DAC=∠ACB,又∵∠DCE=∠B,∴△ADC∽△CAB,得到AC2=AD•BC,求得AC的长度,结合勾股定理,即可构造出关于AB的方程,解方程即可求得相应的AB的长度.
(3)分两种情况来讨论:如图3-1,当BE⊥CE时,∵∠DCE=∠B,∠B+∠BCE=90°,∴∠DCE+∠BCE=90°,作AH⊥BC,则HC=AD=1,∴BH=BC-HC=2-1=1,由sinB即可求得cosB的值,继而求得AB的长度;如图3-2,当BC⊥CE时,延长DA交CE的延长线于点F,由△FDC∽△CEB,可以得到AE的长度,继而求得AB的长度.


| 3 |
| 5 |
| 1 |
| 2 |
(2))由AD∥BC得到∠DAC=∠ACB,又∵∠DCE=∠B,∴△ADC∽△CAB,得到AC2=AD•BC,求得AC的长度,结合勾股定理,即可构造出关于AB的方程,解方程即可求得相应的AB的长度.
(3)分两种情况来讨论:如图3-1,当BE⊥CE时,∵∠DCE=∠B,∠B+∠BCE=90°,∴∠DCE+∠BCE=90°,作AH⊥BC,则HC=AD=1,∴BH=BC-HC=2-1=1,由sinB即可求得cosB的值,继而求得AB的长度;如图3-2,当BC⊥CE时,延长DA交CE的延长线于点F,由△FDC∽△CEB,可以得到AE的长度,继而求得AB的长度.


解答:解:(1)如图1,作AM∥DC交BC于点M,作AH⊥BC于点H,
∵AD∥BC,∴AMCD为平行四边形,
∴AM=DC,MC=AD=1,
∴BM=BC-MC=2-1=1,
∵四边形ABCD为等腰梯形,
∴AB=DC,∴AB=AM,∴BH=HM=
BM=
在直角三角形ABH中,
∵sinB=
=
,
∴cosB=
,∵
=
,∴AB=
.

(2)如图2,∵AD∥BC,
∴∠DAC=∠ACB,
又∵∠DCE=∠B,
∴△ADC∽△CAB,
∴
=
,
∴AC2=AD•BC=2,
作AF⊥BC于点F,
设AB=x,∵sinB=
,
∴AF=
x,BF=
x,
∴CF=2-
x,
在直角三角形AFC中,AF2+CF2=AC2,即:(
x)2+(2-
x)2=2,
∴x=
,
即当点A与点E重合时,AB=
,或者AB=
.

(3)∵△BCE为直角三角形,
∴BE⊥CE或BC⊥CE,
情况一,当BE⊥CE时,如图3-1,
∵∠DCE=∠B,∠B+∠BCE=90°,
∴∠DCE+∠BCE=90°,
作AH⊥BC,则HC=AD=1,
∴BH=BC-HC=2-1=1,
又由sinB=
可得,cosB=
=
=
,
解得:AB=
.

情况二,当BC⊥CE时,如图3-2,
延长DA交CE的延长线于点F,设AE=a,则AF=
a,EF=
a,
在直角三角形BCE中,
∵BC=2,sinB=
,
∴BE=
,EC=
,
∵AD∥BC,BC⊥CE,
∴AD⊥EC,
又∵∠DCE=∠B,
∴△FDC∽△CEB,
∴
=
,即:DF•BC=FC•CE,
∴2×(1+
a)=
×(
+
a),
∴a=
.
∴AB=
+
=
∴当△BCE为直角三角形时,AB=
,或者AB=
.

∵AD∥BC,∴AMCD为平行四边形,
∴AM=DC,MC=AD=1,
∴BM=BC-MC=2-1=1,
∵四边形ABCD为等腰梯形,
∴AB=DC,∴AB=AM,∴BH=HM=
| 1 |
| 2 |
| 1 |
| 2 |
在直角三角形ABH中,
∵sinB=
| AH |
| AB |
| 3 |
| 5 |
∴cosB=
| BH |
| AB |
| BH |
| AB |
| 4 |
| 5 |
| 5 |
| 8 |

(2)如图2,∵AD∥BC,
∴∠DAC=∠ACB,
又∵∠DCE=∠B,
∴△ADC∽△CAB,
∴
| AD |
| AC |
| AC |
| BC |
∴AC2=AD•BC=2,
作AF⊥BC于点F,
设AB=x,∵sinB=
| AH |
| AB |
∴AF=
| 3 |
| 5 |
| 4 |
| 5 |
∴CF=2-
| 4 |
| 5 |
在直角三角形AFC中,AF2+CF2=AC2,即:(
| 3 |
| 5 |
| 4 |
| 5 |
∴x=
8±
| ||
| 5 |
即当点A与点E重合时,AB=
8+
| ||
| 5 |
8-
| ||
| 5 |

(3)∵△BCE为直角三角形,
∴BE⊥CE或BC⊥CE,
情况一,当BE⊥CE时,如图3-1,
∵∠DCE=∠B,∠B+∠BCE=90°,
∴∠DCE+∠BCE=90°,
作AH⊥BC,则HC=AD=1,
∴BH=BC-HC=2-1=1,
又由sinB=
| 3 |
| 5 |
| BH |
| AB |
| 1 |
| AB |
| 4 |
| 5 |
解得:AB=
| 5 |
| 4 |

情况二,当BC⊥CE时,如图3-2,
延长DA交CE的延长线于点F,设AE=a,则AF=
| 4 |
| 5 |
| 3 |
| 5 |
在直角三角形BCE中,
∵BC=2,sinB=
| 3 |
| 5 |
∴BE=
| 5 |
| 2 |
| 3 |
| 2 |
∵AD∥BC,BC⊥CE,
∴AD⊥EC,
又∵∠DCE=∠B,
∴△FDC∽△CEB,
∴
| DF |
| CE |
| FC |
| BC |
∴2×(1+
| 4 |
| 5 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
∴a=
| 5 |
| 14 |
∴AB=
| 5 |
| 14 |
| 5 |
| 2 |
| 20 |
| 7 |
∴当△BCE为直角三角形时,AB=
| 5 |
| 4 |
| 20 |
| 7 |

点评:本题主要考查了相似三角形的判定与性质的综合应用,解答本题的关键在于学会用分类讨论和类比的思想解决问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
用一平面去截下列几何体,其截面可能是长方形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
分式方程
=
的解为( )
| x-2 |
| x |
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
 如图,4根外形相同的小木棒放在圆柱型木桶内,长度分别为12,12,14,15(单位:cm),且露出的部分一样长,然后用纸片盖住.现从木桶中随机取出一根,然后在剩下的3根木棒中又随机取出一根.用树形图或列表法求两次取出的小木棒长度相同的概率.
如图,4根外形相同的小木棒放在圆柱型木桶内,长度分别为12,12,14,15(单位:cm),且露出的部分一样长,然后用纸片盖住.现从木桶中随机取出一根,然后在剩下的3根木棒中又随机取出一根.用树形图或列表法求两次取出的小木棒长度相同的概率.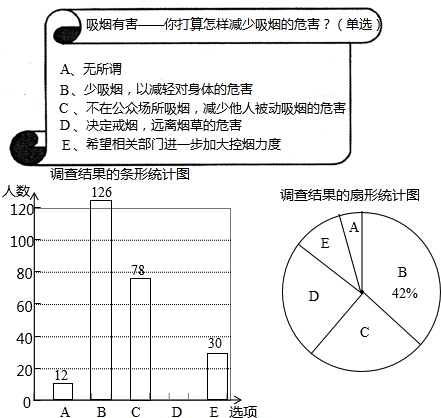
 对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表:
对11月份本社接待的外地游客来杭州旅游的首选景点作了一次抽样调查. 调查结果如下图表: 如图,已知⊙O的直径CD的长为2,
如图,已知⊙O的直径CD的长为2,
 如图,已知△ABC中,AB=AC,∠A=36°.
如图,已知△ABC中,AB=AC,∠A=36°.