题目内容
8.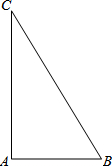 如图,△ABC是直角三角形,∠A=90°,AB=6,AC=8
如图,△ABC是直角三角形,∠A=90°,AB=6,AC=8(1)请画出△ABC的内切圆,圆心为O;
(2)请计算出⊙O的半径.
分析 (1)首先由三角形的内心是三角形三个角平分线的交点,确定圆心,然后作边的垂线,确定半径,继而可求得△ABC的内切圆;
(2)首先利用勾股定理计算出BC长,再由直角三角形的面积等于其内切圆的半径与周长积的一半,即可求得△ABC的内切圆的半径.
解答 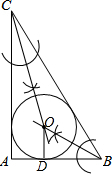 解:(1)①分别作出∠BAC与∠ABC的角平分线,这两条角平分线的交点是△ABC的内切圆的圆心O,
解:(1)①分别作出∠BAC与∠ABC的角平分线,这两条角平分线的交点是△ABC的内切圆的圆心O,
②过点O作OD⊥BA于点D,
③以O为圆心,OD长为半径画圆,
则⊙O即是△ABC的内切圆;
(2)设△ABC内切圆的半径为r,
∵在Rt△ABC中,∠ACB=90°,AB=6,AC=6,
∴CB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴S△ABC=$\frac{1}{2}$AC•BA=$\frac{1}{2}$×8×6=24,AB+AC+BC=24,
∵S△ABC=$\frac{1}{2}$(AB+AC+BC)r,
∴r=$\frac{2{S}_{△ABC}}{AB+AC+BC}$=$\frac{2×24}{24}$=2.
点评 此题考查了三角形的内切圆与内心的性质以及直角三角形的性质.关键是正确确定圆心位置和半径,掌握直角三角形的面积等于其内切圆的半径与周长积的一半.

练习册系列答案
相关题目
20.某养殖户的养殖成本逐年增长,已知第一年的养殖成本为12万元,第3年的养殖成本为17万元.设每年平均增长的百分率为x,则下面所列方程中正确的是( )
| A. | 12(1-x)2=17 | B. | 17(1-x)2=12 | C. | 17(1+x)2=12 | D. | 12(1+x)2=17 |
18.一架a米长的梯子斜靠在墙上,测得它与地面夹角为θ,则梯子底端到墙的距离为( )
| A. | asinθ | B. | acosθ | C. | $\frac{a}{tanθ}$ | D. | $\frac{a}{cosθ}$ |
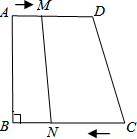 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则: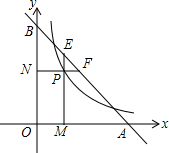 如图,直线y=4-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{2}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,则AF•BE=4.
如图,直线y=4-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{2}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于点F,则AF•BE=4.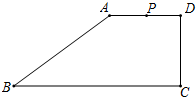 已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),
已知在梯形ABCD中,AD∥BC,∠ADC=90°,且AD=DC=3cm,AB=5cm,动点P从A点出发,以1cm/s的速度沿折线A-D-C运动,过点P作PQ∥AB,交BC于点Q,设运动时间为t(s),