题目内容
14.(1)如图(a),如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系?为什么?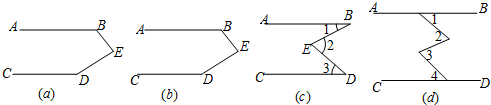
解:过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°(两直线平行,同旁内角互补)
因为∠ABD+∠BED+∠EDC=360°(已知)
所以∠FED+∠EDC=180°(等式的性质)
所以EF∥CD(同旁内角互补,两直线平行)
所以AB∥CD时,∠1,∠2,∠3,∠4满足∠1+∠3=∠2+∠4.
分析 过点E作EF∥AB,由平行线的性质可得出∠ABE+∠BEF=180°,∠ABD+∠BED+∠EDC=360°可得出∠FED+∠EDC=180°,故可得出FE∥CD,由此可得出结论.
解答 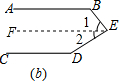 解:过点E作EF∥AB,如图(b),
解:过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°(两直线平行,同旁内角互补 ).
因为∠ABD+∠BED+∠EDC=360°(已知),
所以∠FED+∠EDC=180°(等式的性质),
所以EF∥CD(同旁内角互补,两直线平行),
所以AB∥CD时,∠1,∠2,∠3,∠4满足∠1+∠3=∠2+∠4.
故答案为:两直线平行,同旁内角互补,180,等式的性质,同旁内角互补,两直线平行,∠1+∠3=∠2+∠4.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.

练习册系列答案
相关题目
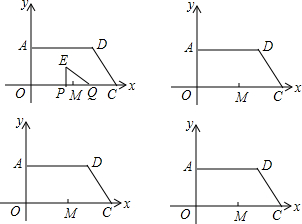
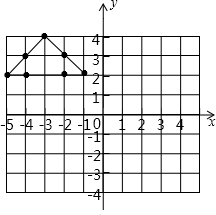 如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化:
如图所示,将图中的点(-5,2),(-3,4),(-1,2),(-4,2),(-2,2),(-2,3),(-4,3)做如下变化: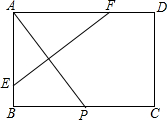 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.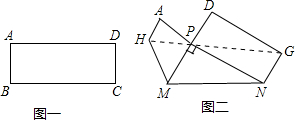 把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,
把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,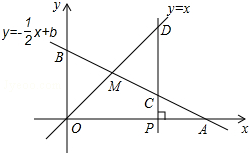 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.