题目内容
3.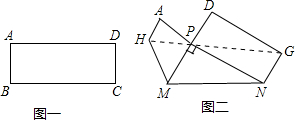 把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,
把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,(1)BC=12;
(2)长方形纸片ABCD的面积为28.8.
分析 ①根据折叠的性质,得BC的长即为MP+MN+NP的长,根据勾股定理求得MN的长即可;
②要求长方形的面积,在①的基础上,关键是求得AB的长,即等于直角三角形MPN斜边上的高,即为直角三角形两条直角边的乘积除以斜边.
解答 解:①∵∠MPN=90°,PM=3,PN=4,
∴MN=5,
∴BC=MP+MN+NP=12,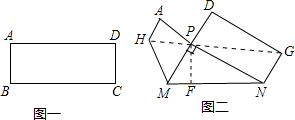
故答案为:12;
②作PF⊥MN于F,
则AB=PF=$\frac{PM•PN}{MN}$=2.4,
则长方形纸片ABCD的面积=AB•BC=28.8,
故答案为:28.8.
点评 此题主要考查了折叠的性质、勾股定理以及直角三角形的面积公式,利用直角三角形两条直角边的乘积除以斜边得斜边的高是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
11.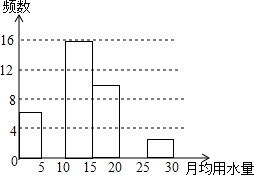 八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
(1)求出a,b的值,并把频数分布直方图补充完整.
(2)求月均用水量不超过15t的家庭数占被调查家庭总数的百分比.
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
 八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | b |
| 25<x≤30 | 2 | 0.04 |
(2)求月均用水量不超过15t的家庭数占被调查家庭总数的百分比.
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表,从表中可知,下列说法错误的是( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -10 | -4 | 0 | 2 | 2 | … |
| A. | 抛物线的对称轴为x=$\frac{1}{2}$ | |
| B. | 抛物线与x轴的另一个交点为(2,0) | |
| C. | 抛物线与直线y=2的两个交点之间的距离为1 | |
| D. | 在对称轴右侧,y随x增大而增大 |
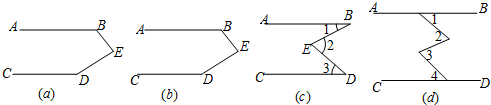
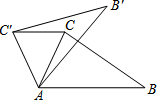 如图,将△ABC绕点A逆时针旋转40°到△AB′C′的位置,则∠ACC′=70°.
如图,将△ABC绕点A逆时针旋转40°到△AB′C′的位置,则∠ACC′=70°.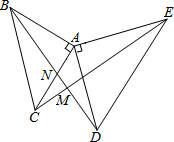 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.