��Ŀ����
3����ͼ1��2��A��B��y���ϵ����㣨��A�ڵ�B���ϱߣ���C��D��x���ϵ����㣨��C�ڵ�D����ߣ���E��F�ֱ���BC��AD���е㣮��1����ͼ1������C��x��Ĵ��߽�AE���ӳ����ڵ�P����֤��AB=PC��
��2����ͼ1������EF����AB=4��CD=2����EF�ij���
��3����ͼ2����AB=CD�����߶�AB��CD�ֱ���y�ᡢx���ϻ���ʱ��ֱ��EF��x��������ļнǡϦ��Ĵ�С�Ƿ�ᷢ���仯�����仯������˵�����ɣ������䣬��������Ϧ��Ĵ�С��

���� ��1����֤��AB=PC��ֻҪ֤����ABE�ա�PCE���ɣ�
��2����ͼ1�У�����DP�������DP����������������λ�߶������ɽ����
��3�����ۣ��Ϧ��Ĵ�С���䣬�Ϧ�=45�㣮��ͼ2�У�����C��x��Ĵ��߽�AE���ӳ����ڵ�P���ɣ�1����֪CP=AB=CD���ٸ���ƽ���ߵ����ʼ��ɽ�����⣮
��� ��1��֤������OA��OD��PC��OD��
��AB��PC��
���EAB=��EPC��
�ڡ�ABE�͡�PCE�У�
$\left\{\begin{array}{l}{��BAE=��EPC}\\{��AEB=��PEC}\\{BE=EC}\end{array}\right.$��
���ABE�ա�PCE��
��AE=EP��
��2����ͼ1�У�����DP��
�ߡ�AEB�ա�PEC��
��AE=EP��
��CP=AB=4��CD=2��
��DP=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$��
��E��F�ֱ���AP��AD�е㣬
��EF=$\frac{1}{2}$DP=$\sqrt{5}$��
��3�����ۣ��Ϧ��Ĵ�С���䣬�Ϧ�=45��
���ɣ���ͼ2�У�����C��x��Ĵ��߽�AE���ӳ����ڵ�P��
�ɣ�1����֪��CP=AB=CD��
���CDP=45�㣬
��EF��DP��
��Ϧ�=��CDP=45�㣮
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����ɶ�������������λ�߶�����֪ʶ������Ĺؼ���ѧ�����ã�1����֤�����������Ӹ����߹���ȫ�������ν�����⣬�����п��������ͣ�

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�| A�� | 3 | B�� | 4 | C�� | 11 | D�� | 6 |
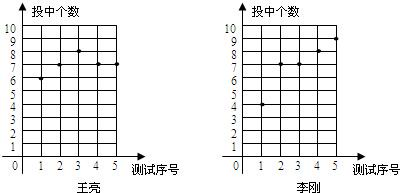
��1���������ͼ�е����ݣ���д����
| ���� | ƽ���� | ���� | ���� |
| ���� | 7 | 7 | 0.4 |
| ��� | 7 | 7 | 2.8 |
 ��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬��D��BC��һ�㣬DE��AB��AE��BC��DE�ֱ�AC��AE�ڵ�O��E������AD��CE��
��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬��D��BC��һ�㣬DE��AB��AE��BC��DE�ֱ�AC��AE�ڵ�O��E������AD��CE��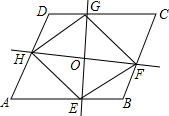 ��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ�������
��ͼ����?ABCD�ĶԽ���AC���е�O�����������ഹֱ��ֱ�ߣ��ֱ�AB��BC��CD��DA��E��F��G��H�ĵ㣬����EF��FG��GH��HE���������ĸ����ۣ���OH=OF���ڡ�HGE=��FGE����S�ı���DHOG=S�ı���BFOE���ܡ�AHO�ա�AEO��������ȷ���ǣ������� С����һ�������εIJ�����ˤ�����ͼ��ʾ���Ŀ飨��ͼ�б���1��2��3��4���Ŀ飩����ֻ��һ�����ԭ��һ����С�������Σ���Ӧ�ô���2�飮
С����һ�������εIJ�����ˤ�����ͼ��ʾ���Ŀ飨��ͼ�б���1��2��3��4���Ŀ飩����ֻ��һ�����ԭ��һ����С�������Σ���Ӧ�ô���2�飮