题目内容
8.已知关于x的一元二次方程x2-(2m-1)x+m2=0有两个实数根x1和x2(1)求实数m的取值范围;
(2)若x1+x2=-1,求m的值.
分析 (1)若一元二次方程有两实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,求出m的取值范围;
(2)由根与系数的关系可以得到x1+x2=2m-1=-1,据此即可求得m的值.
解答 解:(1)由题意有△=[-(2m-1)]2-4m2≥0,
解得m≤$\frac{1}{4}$,
故实数m的取值范围是m≤$\frac{1}{4}$;
(2)由根与系数的关系,得x1+x2=2m-1=-1,
解得m=0,
0<$\frac{1}{4}$,符合题意.
即m的值为0.
点评 本题考查了一元二次方程根的判别式及根与系数的关系,利用两根关系得出的结果必须满足△≥0的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.某种商品每件的进价为190元,按标准的九折销售时.利润率为15.2%,设这种商品的标价为每件x元,依题意列方程正确的是( )
| A. | 0.9x-190=190×0.152 | B. | 0.9x=190×0.152 | ||
| C. | 0.152x=190×0.9 | D. | 190-0.9x=190×0.152 |
17.如图,∠1>∠2的是( )
| A. |  | B. |  | C. |  | D. |  |
 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.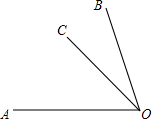 (1)下面是马虎同学解的一道题
(1)下面是马虎同学解的一道题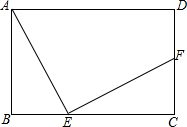 如图,已知长方形ABCD的周长为20,AB=4,点E在BC上,AE⊥EF,AE=EF,求CF的长.
如图,已知长方形ABCD的周长为20,AB=4,点E在BC上,AE⊥EF,AE=EF,求CF的长.