题目内容
18.画网格三角形,并借用网格计算它的面积.(1)每个小正方形的边长为1,三边为$\sqrt{5}$,2$\sqrt{2}$,$\sqrt{17}$.
(2)每个小正方形的边长为a,三边为$\sqrt{17}$a,$\sqrt{13}$a,2$\sqrt{2}$a
(3)每个小长方形长宽为m,n,三边为$\sqrt{{m}^{2}+4{n}^{2}}$,$\sqrt{9{m}^{2}+{n}^{2}}$,$\sqrt{4{m}^{2}+9{n}^{2}}$
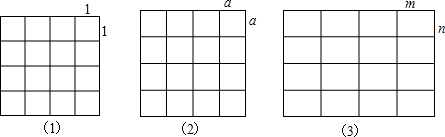
分析 (1)画出直角边为2和1的斜边为$\sqrt{5}$,直角边为2和2的斜边为2$\sqrt{2}$,直角边为4和1的斜边为$\sqrt{17}$,再用长方形的面积减去三个小直角三角形的面积;
(2)画出直角边为4a和a的斜边为$\sqrt{17}$a,直角边为2a和3a的斜边为$\sqrt{13}$a,直角边为2a和2a的斜边为2$\sqrt{2}$a,再用长方形的面积减去三个小直角三角形的面积
(3)画出直角边为m和2n的斜边为$\sqrt{{m}^{2}+4{n}^{2}}$,直角边为3m和n的斜边为$\sqrt{9{m}^{2}+{n}^{2}}$,直角边为2m和3n的斜边为$\sqrt{4{m}^{2}+9{n}^{2}}$,再用长方形的面积减去三个小直角三角形的面积.
解答 解:如图所示: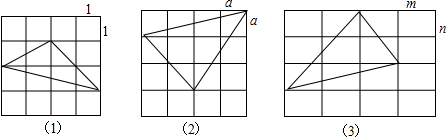
(1)面积为:4×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×1-$\frac{1}{2}$×2×2
=8-1-2-2
=3;
(2)面积为:4a×3a-$\frac{1}{2}$×4a×a-$\frac{1}{2}$×2a×2a-$\frac{1}{2}$×3a×2a
=12a2-2a2-2a2-3a2
=5a2;
(3)面积为:3m×3n-$\frac{1}{2}$×2m×3n-$\frac{1}{2}$×m×2n-$\frac{1}{2}$×3m×n
=9mn-3mn-mn-1.5mn
=3.5mn.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.同时考查了面积计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.方程x(x-1)=x的根是( )
| A. | x1=2,x2=0 | B. | x=-2 | C. | x1=-2,x2=0 | D. | x=2 |
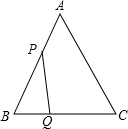 如图,在△ABC中.AB=AC=5cm,BC=6cm,点P从点沿AB向点B运动,点Q从点B沿BC向点C运动,速度都为1cm/s,P、Q两点同时出发,当点P到达点B时,运动停止,求运动几秒时,点P与点Q的连线PQ与△ABC的边垂直.
如图,在△ABC中.AB=AC=5cm,BC=6cm,点P从点沿AB向点B运动,点Q从点B沿BC向点C运动,速度都为1cm/s,P、Q两点同时出发,当点P到达点B时,运动停止,求运动几秒时,点P与点Q的连线PQ与△ABC的边垂直. 如图,在六边形ABCDEF中,AF∥CD,且∠A=120°,∠B=80°,∠E+∠F=260°,求∠C与∠D的度数.
如图,在六边形ABCDEF中,AF∥CD,且∠A=120°,∠B=80°,∠E+∠F=260°,求∠C与∠D的度数. 如图,已知E为?ABCD的边CD上一点,BE交AD的延长线于点F.若S?ABCD:S△AEF=5:1,求$\frac{AF}{DF}$的值.
如图,已知E为?ABCD的边CD上一点,BE交AD的延长线于点F.若S?ABCD:S△AEF=5:1,求$\frac{AF}{DF}$的值.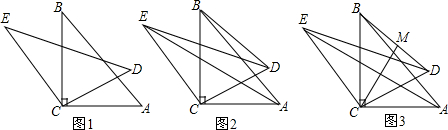
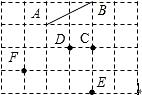 如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的所有线段中,与线段AB平行的线段是FD,与线段AB垂直的线段是DE.
如图,在4×6的正方形网格,点A、B、C、D、E、F都在格点上,连接C、D、E、F中任意两点得到的所有线段中,与线段AB平行的线段是FD,与线段AB垂直的线段是DE.