题目内容
18. 写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.
写出下列各函数的表达式.指出它是什么函数,并确定函数的自变量的取值范围.(1)矩形的周长为20cm,它的面积S(cm2)是它的一边长a(cm)的函数.
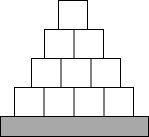
(2)如图,最下面是一个长方形,上面是10个小正方形.如果长方形的长为4cm,宽为小正方形长的一半,那么这个图形的总面积S(cm2)是每个小正方形的边长x(cm)的函数.
分析 (1)根据矩形的周长为20cm,它的一边长为acm,得出另一边长为(10-a)cm,利用矩形的面积公式,可得函数关系式,进而求解即可;
(2)根据图形的总面积=长方形的面积+10个正方形的面积,进而求解即可.
解答 解:(1)∵矩形的周长为20cm,它的一边长为acm,
∴另一边长为(10-a)cm,
∴S=a(10-a)=-a2+10a,S是a的二次函数,
∵$\left\{\begin{array}{l}{a>0}\\{10-a>0}\end{array}\right.$,
∴0<a<10;
(2)由题意得,S=4×$\frac{1}{2}$x+10x2,
即S=2x+10x2,S是x的二次函数,
∵$\left\{\begin{array}{l}{x>0}\\{4x≤4}\end{array}\right.$,
∴0<x≤1.
点评 本题考查了根据实际问题列二次函数关系式,二次函数的定义,正确理解题意,掌握矩形与正方形的面积公式是解题的关键.

练习册系列答案
相关题目
7.CD为△ABC的高且∠A:∠B:∠C=1:2:3,AB=m,则CD等于( )
| A. | $\frac{m}{2}$ | B. | $\frac{m}{4}$ | C. | $\frac{\sqrt{3}}{4}$m | D. | $\frac{\sqrt{3}}{2}$m |
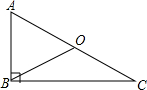 如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.
如图,已知Rt△ABC,∠ABC=90°,BO是斜边AC上的中线.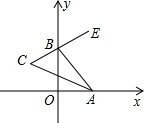 如图,已知∠xOy=90°,点A、B分别在x轴、y轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,问:∠C的大小是否发生变化?如果保持不变,求出∠C的大小,如果随点A、B的移动发生变化,请求出∠C的变化范围.
如图,已知∠xOy=90°,点A、B分别在x轴、y轴上移动,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,问:∠C的大小是否发生变化?如果保持不变,求出∠C的大小,如果随点A、B的移动发生变化,请求出∠C的变化范围.