题目内容
等腰三角形的底边长为24,腰长为13,则这个等腰三角形底边上的高是 ,面积是 ,腰上的高长是 .
考点:勾股定理,等腰三角形的性质
专题:
分析:根据题意画出图形,过点A作AD⊥BC于点D,根据等腰三角形的性质得出BD的长,由勾股定理求出AD的长,根据三角形的面积公式即可得出其面积.再设上的高长是h,根据三角形的面积公式即可得出h的值.
解答: 解:如图所示,过点A作AD⊥BC于点D,
解:如图所示,过点A作AD⊥BC于点D,
∵AB=AC=12,BC=24,
∴BD=
BC=12,
∴AD=
=
=5,
∴S△ABC=
BC•AD=
×24×5=60.
设腰上的高长是h,则
AB•h=60,即
×13h=60,解得h=
.
故答案为:5,60,
.
 解:如图所示,过点A作AD⊥BC于点D,
解:如图所示,过点A作AD⊥BC于点D,∵AB=AC=12,BC=24,
∴BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 132-122 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
设腰上的高长是h,则
| 1 |
| 2 |
| 1 |
| 2 |
| 120 |
| 13 |
故答案为:5,60,
| 120 |
| 13 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
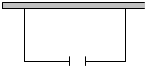 用篱笆围成一个长方形的花坛,其中一面靠墙,且在与墙平行的一边开一扇1米宽的门,如果墙长7米,现在有12米的篱笆,花坛的面积需要20平方米,求花坛的长和宽.
用篱笆围成一个长方形的花坛,其中一面靠墙,且在与墙平行的一边开一扇1米宽的门,如果墙长7米,现在有12米的篱笆,花坛的面积需要20平方米,求花坛的长和宽.