题目内容
4. 如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G.
如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G.(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FO•ED=OD•EF.
分析 (1)根据已知条件可得到GF∥AD,则有$\frac{GF}{AD}$=$\frac{EF}{ED}$,由BF∥CD可得到$\frac{BF}{CD}$=$\frac{EF}{ED}$,又因为AD=CD,可得到GF=FB;
(2)延长GF交AM于H,根据平行线分线段成比例定理得到$\frac{GF}{BE}=\frac{FH}{BM}$,由于BM=BE,得到GF=FH,由GF∥AD,得到$\frac{EF}{ED}=\frac{GF}{AD},\frac{FH}{AD}=\frac{FO}{OD}$,等量代换得到$\frac{EF}{ED}=\frac{FH}{AD}$,即$\frac{EF}{ED}=\frac{FO}{OD}$,于是得到结论.
解答 证明:(1)∵四边形ABCD是正方形,
∴AD∥BC,AB∥CD,AD=CD,
∵GF∥BE,
∴GF∥BC,
∴GF∥AD,
∴$\frac{GF}{AD}=\frac{EF}{ED}$,
∵AB∥CD,
∴$\frac{BF}{CD}=\frac{EF}{ED}$,
∵AD=CD,
∴GF=BF;
(2)延长GF交AM于H,
∵GF∥BC,
∴FH∥BC,
∴$\frac{GF}{BE}=\frac{AF}{AB},\frac{FH}{BM}=\frac{AF}{AB}$,
∴$\frac{GF}{BE}=\frac{FH}{BM}$,
∵BM=BE,
∴GF=FH,
∵GF∥AD,
∴$\frac{EF}{ED}=\frac{GF}{AD},\frac{FH}{AD}=\frac{FO}{OD}$,
∴$\frac{EF}{ED}=\frac{FH}{AD}$,
∴$\frac{EF}{ED}=\frac{FO}{OD}$,
∴FO•ED=OD•EF.
点评 本题主要考查平行线分线段成比例及正方形的性质,掌握平行线分线段中的线段对应成比例是解题的关键,注意利用比例相等也可以证明线段相等.

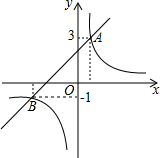 如图,直线l:y=x+2与双曲线C:y=$\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.
如图,直线l:y=x+2与双曲线C:y=$\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1. 如图,已知∠1=∠2,要使△ABD≌△ACD,则要添加的一个条件是∠B=∠C.
如图,已知∠1=∠2,要使△ABD≌△ACD,则要添加的一个条件是∠B=∠C.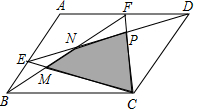 如图所示,在平行四边形ABCD中,E、F分别为AB和AD上的两个动点.
如图所示,在平行四边形ABCD中,E、F分别为AB和AD上的两个动点.