Question

14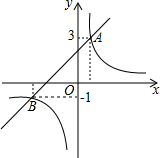．如图，直线l：y=x+2与双曲线C：y=$\frac{k}{x}$相交于A，B两点其中点A的纵坐标为3，点B的纵坐标为-1．
（1）写出双曲线C的表达式；
（2）过动点P（n，0）且垂直于x轴的直线与l和C的交点分别为M，N，当点M位于点N的上方时，写出n的取值范围．

Answer 1

分析 （1）将点A的纵坐标为3，点B的纵坐标为-1代入y=x+2得出两点坐标，再代入y=$\frac{k}{x}$，得出k的值，从而得出双曲线C的表达式；
（2）根据题意得出当点M位于点N的上方时，得出-3＜x＜0或x＞1，再分类讨论：①3＜x＜0时，x＞1时即可．

解答 解：（1）∵直线交双曲线于A，B两点
∴将y=3代入 y=x+2，得x=1，
∴A（1，3 ），B（-3，-1），
把 A（1，3 ） 代入y=$\frac{k}{x}$得k=3，
∴y=$\frac{3}{x}$；

（2）由已知得，结合图示，x＜-3时点 M  都位于点 N  的下方，
x=-3时，M，N重合，
-3＜x＜0时，点 M  都位于点 N  的上方，
0＜x＜1时，点 M  都位于点 N  的下方，
x=1时，M，N重合，
x＞1时，点 M  都位于点 N  的上方，
∴n的取值范围是-3＜x＜0或x＞1．

点评 本题考查了反比例函数和一次函数的交点问题，掌握用待定系数法求函数的解析式是解题的关键．