题目内容
17.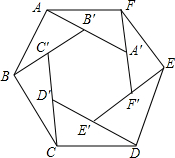 如图所示,六边形ABCDEF是正六边形,且与六边形A′B′C′D′E′F′相似,如果A′、B、′C′、D′、E′、F′分别在AB′、BC′、CD′、DE′、EF′、FA′上,求证:△ABB′≌△BCC′≌△CDD′≌△DEE′≌△EFF′≌△FAA′.
如图所示,六边形ABCDEF是正六边形,且与六边形A′B′C′D′E′F′相似,如果A′、B、′C′、D′、E′、F′分别在AB′、BC′、CD′、DE′、EF′、FA′上,求证:△ABB′≌△BCC′≌△CDD′≌△DEE′≌△EFF′≌△FAA′.
分析 根据六边形ABCDEF是正六边形,且与六边形A′B′C′D′E′F′相似,于是得到∠A′B′C′=∠B′A′F′=∠BAF=120°,求得∠ABB′=∠A′AF,推出△ABB′≌△FAA′,于是得到结论.
解答 证明:∵六边形ABCDEF是正六边形,且与六边形A′B′C′D′E′F′相似,
∴∠A′B′C′=∠B′A′F′=∠BAF=120°,
∴∠AB′B=∠FA′A=60°,
∠FAB′+∠BAB′=∠ABB′+∠BAB′=120°,
∴∠ABB′=∠A′AF,
∵AB=AF,
在△ABB′与△FAA′中,$\left\{\begin{array}{l}{∠ABB′=∠FAA′}\\{∠BB′A=∠AA′F}\\{AB=AF}\end{array}\right.$,
∴△ABB′≌△FAA′,
同理:△ABB′≌△BCC′≌△CDD′≌△DEE′≌△EFF′≌△FAA′.
点评 本题考查了全等三角形的判定,正六边形的性质,相似多边形的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有理数a,b,c在数轴上的相应位置如图所示,化简|a|+|b|-|c|.
有理数a,b,c在数轴上的相应位置如图所示,化简|a|+|b|-|c|.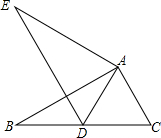 如图,已知△ABC≌△AED,∠E=∠B,∠C=∠ADE,若∠BAD=$\frac{1}{3}$∠EAD=30°,求∠DAC的度数.
如图,已知△ABC≌△AED,∠E=∠B,∠C=∠ADE,若∠BAD=$\frac{1}{3}$∠EAD=30°,求∠DAC的度数.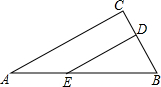 如图,在Rt△ABC中,∠C=90°,ED⊥BC,D为垂足,BD=3cm,DC=2cm,AB=6cm.求BE和EA的长.
如图,在Rt△ABC中,∠C=90°,ED⊥BC,D为垂足,BD=3cm,DC=2cm,AB=6cm.求BE和EA的长. 如图,△ABC在平面直角坐标系中三个顶点的坐标分别为A(1,1),B(2,-1),C(3,0)
如图,△ABC在平面直角坐标系中三个顶点的坐标分别为A(1,1),B(2,-1),C(3,0)