题目内容
12．
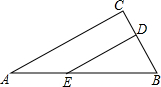如图，在Rt△ABC中，∠C=90°，ED⊥BC，D为垂足，BD=3cm，DC=2cm，AB=6cm．求BE和EA的长．
分析 由∠C=90°，ED⊥BC，得到∠EDB=∠C=90°，证得DE∥AC，根据平行线分线段成比例定理即可得到结论．
解答 解：∵∠C=90°，ED⊥BC，
∴∠EDB=∠C=90°，
∴DE∥AC，
∴$\frac{BD}{BC}=\frac{BE}{AB}$，
∴$\frac{3}{5}=\frac{BE}{6}$，
∴BE=$\frac{18}{5}$，
∴AE=AB-BE=$\frac{12}{5}$．
点评 本题考查了平行线分线段成比例，熟练掌握平行线分线段成比例定理是解题的关键．
练习册系列答案
相关题目
2．地球与太阳的距离约为150000000千米；将数字150000000用科学记数法表示为（ ）
| A． | 15×107千米 | B． | 1.5千米 | C． | 1.5×108千米 | D． | 0.15×107千米 |
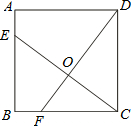如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD=$\frac{4}{3}$，④S△ODC=S四边形BEOF中，正确的有①③④．
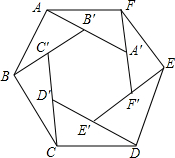如图所示，六边形ABCDEF是正六边形，且与六边形A′B′C′D′E′F′相似，如果A′、B、′C′、D′、E′、F′分别在AB′、BC′、CD′、DE′、EF′、FA′上，求证：△ABB′≌△BCC′≌△CDD′≌△DEE′≌△EFF′≌△FAA′．