题目内容
15．用配方法证明：不论a取任何实数，下列代数式都成立．（1）a2-6a+17的值一定为正；
（2）-x2+4x-5的值一定小于零．
分析 （1）直接配上一次项系数的一半的平方，再进一步利用非负数的性质证明即可；
（2）先两前面两项提-1得到x2-4x+5，再利用配方法得到-（x-2）2-1，然后根据非负数的性质进行证明．
解答 证明：（1）a2-6a+17=（a-3）2+8，
∵（a-3）2≥0，
∴（a-3）2+8＞0，
即a2-6a+17的值一定为正．
（2）-x2+4x-5=-（x2-4x+5）=-（x-2）2-1，
∵（x-2）2≥0，
∴-（x-2）2≤0，
∴-（x-2）2-1＜0，
即-x2+4x-5的值一定小于零．
点评 此题考查配方法的运用，解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
名校课堂系列答案
相关题目
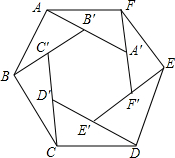如图所示，六边形ABCDEF是正六边形，且与六边形A′B′C′D′E′F′相似，如果A′、B、′C′、D′、E′、F′分别在AB′、BC′、CD′、DE′、EF′、FA′上，求证：△ABB′≌△BCC′≌△CDD′≌△DEE′≌△EFF′≌△FAA′．
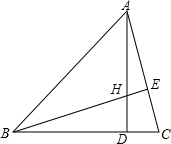如图，△ABC中，H是高AD、BE的交点，且BH=AC，则∠ABC=45°．
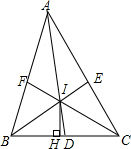如图，在△ABC中，三角形内角平分线AD，BE，CF相交于点I，IH⊥BC于点H，求证：∠BID=∠HIC．