题目内容
15.已知a2+b2-6a-8b=-25,求a、b的值.分析:“若几个非负数的和为零,则这几个非负数皆为零”,当一个等式里含有几个未知数时,若能将该等式化为几个非负数的和的形式,便能利用上述性质来求解.
例如,讲方程a2+b2-6a-8b=-25,化为(a-3)2+(b-4)2=0,从而求得a=3,b=4.
再如,将方程a+b-$2\sqrt{a}$-2$\sqrt{b-1}$+1=0化为a-2$\sqrt{a}$+1+(b-1)2$\sqrt{b-1}$+1=0,
再将方程左边配成两个完全平方式和($\sqrt{a}$-1)2+$\sqrt{b-1}$-1)2=0,从而求得a=1,b=2.
使用类似的方法解决下面的问题:
(1)已知a+b=2$\sqrt{ab}$(a>0,b>0),求$\frac{\sqrt{4a-b}}{\sqrt{5a+7b}}$的值.
(2)已知a+b+c=2$\sqrt{a+1}$+4$\sqrt{b+1}$+6$\sqrt{c-2}$-14.求a、b、c的值.
分析 (1)首先把a+b=2$\sqrt{ab}$两边平方,整理得出(a-b)2=0,得出a=b,进一步代换求得数值即可;
(2)先移项,再利用配方法得到a+1-2$\sqrt{a+1}$+1+b+1-4$\sqrt{b+1}$+4+c-2-6$\sqrt{c-2}$+9=0即有($\sqrt{a+1}$-1)2+($\sqrt{b+1}$-2)2+($\sqrt{c-2}$-3)2=0,然后根据非负数的性质得$\sqrt{a+1}$-1=0,$\sqrt{b+1}$-2=0,$\sqrt{c-2}$-3=0解得a=0,b=3,c=4.
解答 解:(1)∵a+b=2$\sqrt{ab}$,
∴a2+2ab+b2=4ab,
∴(a-b)2=0,
∴a=b,
∴$\frac{\sqrt{4a-b}}{\sqrt{5a+7b}}$=$\sqrt{\frac{3a}{12a}}$=$\sqrt{\frac{1}{4}}$=$\frac{1}{2}$;
(2)∵a+b+c=2$\sqrt{a+1}$+4$\sqrt{b+1}$+6$\sqrt{c-2}$-14,
∴a+1-2$\sqrt{a+1}$+1+b+1-4$\sqrt{b+1}$+4+c-2-6$\sqrt{c-2}$+9=0,
∴($\sqrt{a+1}$-1)2+($\sqrt{b+1}$-2)2+($\sqrt{c-2}$-3)2=0,
∴$\sqrt{a+1}$-1=0,$\sqrt{b+1}$-2=0,$\sqrt{c-2}$-3=0,
∴a+1=1,b+1=4,c-2=3,
∴a=0,b=3,c=4.
点评 本题考查了配方法的应用:用配方法解一元二次方程,配方法的理论依据是公式a2±2ab+b2=(a±b)2;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案| 苹果总量n(千克) | 损坏苹果质量m(千克) | 损坏率$\frac{m}{n}$ |
| 100 | 6.5 | 0.065 |
| 200 | 14 | 0.07 |
| 400 | 23 | 0.0575 |
| 600 | 38 | 0.0633 |
| 1000 | 61 | 0.061 |
| 2000 | 119 | 0.0595 |
| 4000 | 241 | 0.06025 |
(2)如果这个商人将运10000千克“红富士”苹果去新疆,原来在未考虑有损坏时确定的批发价为2元/千克,为了确保原有利润,现在的批发价应上升多少(精确到0.01)?
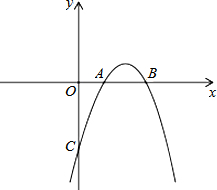 已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).