题目内容
5.已知函数y=(x+1)2-4.(1)若将抛物线先向右平移2个单位长度,再向上平移4个单位长度,求得到的抛物线的解析式;
(2)该抛物线经过怎样的平移能经过原点?
(3)当x取何值时,函数值大于0?当x取何值时,函数值小于0?
分析 (1)根据平移规律“上加下减”直接得到平移后抛物线的解析式;
(2)设经过原点的抛物线解析式为:y=(x+1)2-4+h,把原点坐标代入该解析式求得h的值;
(3)根据抛物线的性质解答.
解答 解:(1)将抛物线y=(x+1)2-4向右平移2个单位长度,再向上平移4个单位长度后得到抛物线的解析式为:y=(x+1-2)2-4+4,即y=(x-1)2;
(2)设经过原点的抛物线解析式为:y=(x+1)2-4+h,
把(0,0)代入,得
0=(0-1)2-4+h,
解得h=3,
则该抛物线解析式为:y=(x+1)2-1;
即把抛物线y=(x+1)2-4向上平移3个单位后的抛物线经过原点;
(3)y=(x+1)2-4=(x+3)(x-1),则该抛物线与x轴的交点横坐标分别是-3,1,且该抛物线的开口方向向上,
所以当x<-3或x>1时,y>0;
当-3<x<1时,y<0.
点评 主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
 如图所示,分别以六边形的顶点为圆心,以2个单位长度为半径画圆,则图中阴影部分的面积之和为多少平方单位?(结果保留π)
如图所示,分别以六边形的顶点为圆心,以2个单位长度为半径画圆,则图中阴影部分的面积之和为多少平方单位?(结果保留π) 有一条长7.2m的木料,做成如图所示的窗框,当窗框的宽最大为多少时,这个窗户的面积为2m2?(不考虑木料加工时的损耗和中间木框所占的面积)
有一条长7.2m的木料,做成如图所示的窗框,当窗框的宽最大为多少时,这个窗户的面积为2m2?(不考虑木料加工时的损耗和中间木框所占的面积)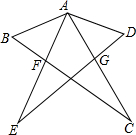 如图,AC=AE,∠C=∠E,∠BAC=∠DAE.求证:
如图,AC=AE,∠C=∠E,∠BAC=∠DAE.求证: