题目内容
2.如图,在△ABC中,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E.(1)若点B、C在DE的同侧(如图(1)),且AD=CE,AE=BD,求证:△ABC为等腰直角三角形.
(2)若点B、C在DE的两侧(如图(2)),其他条件不变,问△ABC为等腰直角三角形吗?若是,请加以证明;若不是,请说明理由.

分析 (1)由已知条件,证明△ABD≌△ACE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC;
(2)同(1),先证△ABD≌△ACE,再利用角与角之间的关系求证∠BAD+∠CAE=90°,即可证明AB⊥AC.
解答 证明:(1)∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
在Rt△ABD和Rt△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=CE}\end{array}\right.$,
∴Rt△ABD≌Rt△CAE.
∴∠DAB=∠ECA,∠DBA=∠ACE.
∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,
∴∠BAD+∠CAE=90°.
∠BAC=180°-(∠BAD+∠CAE)=90°.
∴AB⊥AC.
∴△ABC为等腰直角三角形;
(2)△ABC为等腰直角三角形.理由如下:
同(1)一样可证得Rt△ABD≌Rt△ACE.
∴∠DAB=∠ECA,∠DBA=∠EAC,
∵∠CAE+∠ECA=90°,
∴∠CAE+∠BAD=90°,即∠BAC=90°,
∴AB⊥AC,
∴△ABC为等腰直角三角形.
点评 此题考查全等三角形的判定和性质,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,借助全等三角形的性质得到相等的角,然后证明垂直是经常使用的方法,注意掌握、应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在具备下列条件的△ABC中,不是直角三角形的是( )
| A. | ∠A+∠B=∠C | B. | ∠A=3∠C,∠B=2∠C | C. | ∠A=∠B=2∠C | D. | ∠A=∠B=$\frac{1}{2}$∠C |
 如图,已知:AB∥CD,MG、NH分别平分∠EMB和∠DNM,那么MG与NH平行吗?
如图,已知:AB∥CD,MG、NH分别平分∠EMB和∠DNM,那么MG与NH平行吗? 如图,已知:BE=CD,∠B=∠C,求证:∠1=∠2.
如图,已知:BE=CD,∠B=∠C,求证:∠1=∠2.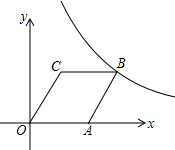 如图,在平面直角坐标系中,菱形OABC的顶点O和顶点A均在x轴上,且点B(8,4)在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系中,菱形OABC的顶点O和顶点A均在x轴上,且点B(8,4)在反比例函数y=$\frac{k}{x}$(x>0)的图象上. 如图,每个小正方形的边长是1,请你在图中画出一个面积是5的正方形.
如图,每个小正方形的边长是1,请你在图中画出一个面积是5的正方形.