题目内容
18.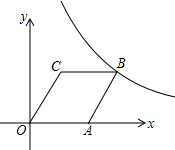 如图,在平面直角坐标系中,菱形OABC的顶点O和顶点A均在x轴上,且点B(8,4)在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系中,菱形OABC的顶点O和顶点A均在x轴上,且点B(8,4)在反比例函数y=$\frac{k}{x}$(x>0)的图象上.(1)求反比例函数的解析式及菱形OABC的长;
(2)若将菱形OABC向上平移m个单位长度,则菱形的顶点C恰好落在反比例函数图象上,求m的值.
分析 (1)把点B的坐标代入反比例函数求出k的值,即可得出反比例函数的解析式;作BD⊥x轴于D,则∠ADB=90°,BD=4,OD=8,由勾股定理得出AD2+BD2=AB2,设AB=OA=BC=x,则AD=8-x,由勾股定理得出方程,解方程求出AB即可;
(2)先由题意得出点C的坐标,将菱形OABC向上平移m个单位长度后点C的坐标为(3,m+4),代入反比例函数解析式,求出m的值即可.
解答 解:(1)把点B(8,4)代入反比例函数y=$\frac{k}{x}$(x>0)得:
k=8×4=32,
∴反比例函数的解析式为:y=$\frac{32}{x}$;
作BD⊥x轴于D,如图所示:
则∠ADB=90°,BD=4,OD=8,
∴AD2+BD2=AB2,
∵四边形OABC是菱形,
∴OA=AB=BC,
设AB=OA=BC=x,
则AD=8-x,
∴(8-x)2+42=x2,
解得:x=5,
∴菱形OABC的边长为5;
(2)∵BC=5,8-5=3,
∴点C的坐标为(3,4),
若将菱形OABC向上平移m个单位长度,
则点C的坐标为(3,m+4),
∵点C恰好落在反比例函数图象上,
∴3(m+4)=32,
解得:m=$\frac{20}{3}$.
即若将菱形OABC向上平移m个单位长度,则菱形的顶点C恰好落在反比例函数图象上,m的值为$\frac{20}{3}$.
点评 本题考查是反比例函数综合题目,考查了反比例函数解析式的求法、勾股定理、坐标与图形性质、菱形的性质、平移的性质等知识;本题综合性强,有一定难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.有理数-1,-(-12),-|-12|,按从小到大的顺序排列为( )
| A. | -1<-(-12)<-|-12| | B. | -(-12)<-|-12|<-1 | C. | -|-12|<-1<-(-12) | D. | -|-12|<-(-12)<-1 |
6.天虹商店打折销售中,某件商品打出“1元换2.5元劵”的促销活动,此活动相当于打几折?( )
| A. | 2.5 | B. | 4 | C. | 6 | D. | 7.5 |
13.某班在体育课上进行1000米测试,在起点处学生小明比小华先跑1分钟,当小明到达终点时,小华还有440米没跑.已知小明每秒钟比小华每秒钟多跑1米.设小华速度为x米/秒,则可列方程为( )
| A. | $\frac{1000}{x+1}$+1=$\frac{1000-440}{x}$ | B. | $\frac{1000}{x+1}$+60=$\frac{1000-440}{x}$ | ||
| C. | $\frac{1000}{x+1}$-1=$\frac{1000-440}{x}$ | D. | $\frac{1000}{x+1}$-60=$\frac{1000-440}{x}$ |
8.若a2-3ab-4b2=0,则$\frac{a}{b}$的值( )
| A. | 1 | B. | -1 | C. | 4或-1 | D. | -4或1 |

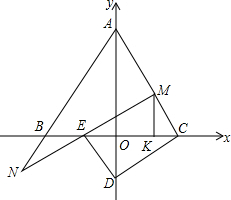 已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE.
已知B(-2,0),C(2,0),点A是y轴正半轴上一点,CD⊥AC交y轴于D,M为AC上一动点.N为AB延长线一动点,且满足AM+AN=2AC,MN交BC于E,连DE. 如图,?ABCD的顶点O为坐标原点,点A在x轴正半轴上,∠COA=60°,OA=10,OC=4,反比例函数的图象在第一象限内过点C.
如图,?ABCD的顶点O为坐标原点,点A在x轴正半轴上,∠COA=60°,OA=10,OC=4,反比例函数的图象在第一象限内过点C.