题目内容
1．解方程组：$\left\{\begin{array}{l}{a+b=8①}\\{4ab=64-4②}\end{array}\right.$．分析 把第一个方程化为b=8-a，再把b=8-a代入第二个方程，可得一个关于a的一元二次方程，解方程，求出a值，再进一步求b即可．
解答 解：$\left\{\begin{array}{l}{a+b=8①}\\{4ab=64-4②}\end{array}\right.$，
由①得，b=8-a③，
把③代入②得，a2-8a+15=0，
解得：a1=3，a2=5，
把a1=3，a2=5代入③得，
b1=5，b2=3，
所以方程组的解为：$\left\{\begin{array}{l}{{a}_{1}=3}\\{{b}_{1}=5}\end{array}\right.$，$\left\{\begin{array}{l}{{a}_{2}=5}\\{{b}_{2}=3}\end{array}\right.$．
点评 解答此类题目一般用代入法比较简单，先消去一个未知数，再解关于另一个未知数的一元二次方程，把求得结果代入一个较简单的方程中即可．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
9．
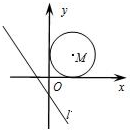如图，已知直线l：y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移；同时以点m（3，3）为圆心，3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移，当直线l与圆m相切时，则运动的时间为（ ）
如图，已知直线l：y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移；同时以点m（3，3）为圆心，3个单位长度为半径的圆m以每秒2个单位长度的速度向右平移，当直线l与圆m相切时，则运动的时间为（ ）| A． | 2.5 | B． | 5-2$\sqrt{2}$ | C． | 2.5或10 | D． | 5-2$\sqrt{2}$或5+2$\sqrt{2}$ |
6．某商场三月份销售某品牌电视机，统计了其中三种型号电视机的销售量如下表显示：
根据本月各种型号电视机的销售全额和各种型号电视机的单价（销售全额=销售量×单价），制作了如下所示的统计图
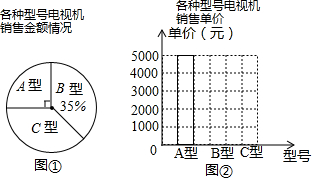
由图解答下列问题：
（1）求该商场三月份销售这三种型号电视机的总销售金额；
（2）求出B，C两种型号电视机的销售单价，并把图②中的条形统计图补充完整；
（3）四月份，该商场三种电视机的销售单价不变，三种型号电视机共销出35台，已知A，B，C三种型号电视机销售数量的中位数是15台，总销售金额为98500元，求A，B，C三种型号电视机在四月份各销售了多少台？
| 电视机型号 | A型 | B型 | C型 |
| 销售量（台） | 5 | 10 | 20 |
由图解答下列问题：
（1）求该商场三月份销售这三种型号电视机的总销售金额；
（2）求出B，C两种型号电视机的销售单价，并把图②中的条形统计图补充完整；
（3）四月份，该商场三种电视机的销售单价不变，三种型号电视机共销出35台，已知A，B，C三种型号电视机销售数量的中位数是15台，总销售金额为98500元，求A，B，C三种型号电视机在四月份各销售了多少台？
13．下列四边形中，是轴对称但不是中心对称的图形是（ ）
| A． | 矩形 | B． | 菱形 | C． | 平行四边形 | D． | 等腰梯形 |