题目内容
12.【背景资料】数学家高斯5岁时,便能熟练计算:1+2+3+…+100,他的方法是:原式=$\frac{1}{2}$(1+2+3+…+100+100+99…+2+1)=$\frac{1}{2}$(100+1)×100.
【问题解决】
(1)请你直接写出结果:1+2+3+…+(n-1)+n=$\frac{n(n+1)}{2}$;
(2)某公司从2012年9月初开始销售中档家用汽车,当月销售额为b万元,以后逐月增加k万元,至开业一周年之际,已累计销售732万元,至今年9月初已累计销售1752万元,今年9月以来,行情猛涨,每月销售额均比上月增长25%,这样,今年9、10两个月的销售额正好等于开业初n个月的累计销售额,求n的值.
分析 (1)根据高斯求和公式即可求解;
(2)根据待定系数法得到月销售额y(万元)与月数x之间的函数关系式,根据今年9、10两个月的销售额正好等于开业初n个月的累计销售额,列出方程求解即可.
解答 解:(1)1+2+3+…+(n-1)+n=$\frac{n(n+1)}{2}$;
(2)设月销售额y(万元)与月数x之间的函数关系式为y=k(x+1)+b,依题意有
$\left\{\begin{array}{l}{k+2k+…+11k+12k=732}\\{k+2k+…+23k+24k=1752}\end{array}\right.$,
即$\left\{\begin{array}{l}{66k+12b=732}\\{12×23k+24b=1752}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{b=50}\end{array}\right.$.
则y=2(x-1)+50=2x+48,
至今年9月初,即x=24时,y=96(万元),
故今年9,10月共销售:96×(1+25%)+96×(1+25%)2=270(万元),
开业初几个月的累计销售额为50n+$\frac{n(n-2)}{2}$×2=n2+49n,
则n2+49n-270=0,
解得n1=5,n2=-54(舍去).
故n的值为5.
故答案为:$\frac{n(n+1)}{2}$.
点评 考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.某县10名学生参加汉字听写大赛,他们得分情况如下表:
那么这10名学生所得分数的中位数和众数分别是( )
| 人数 | 3 | 4 | 2 | 1 |
| 分数 | 80 | 85 | 90 | 95 |
| A. | 85和82.5 | B. | 85.5和85 | C. | 85和85 | D. | 85.5和80 |

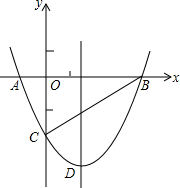 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).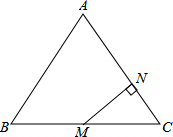 如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,
如图,在△ABC中,AB=AC=5cm,BC=6cm,M为BC中点,MN⊥AC,垂足为N,