题目内容
6.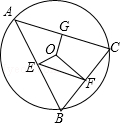 如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.
如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.
分析 连结OC,构建直角三角形:在Rt△OCG中,利用勾股定理可和垂径定理得到AE=BE,BF=CF,则EF为△BAC的中位线,然后根据三角形中位线性质得到EF=$\frac{1}{2}$AC.
解答  解:如图,连结OC,
解:如图,连结OC,
∵OG⊥AC,
∴CG=AG,
在Rt△OCG中,CG=$\sqrt{O{C}^{2}-O{G}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
∴AC=2CG=4$\sqrt{2}$,
∵OE⊥AB,OF⊥BC,
∴AE=BE,BF=CF,
∴EF为△BAC的中位线,
∴EF=$\frac{1}{2}$AC=2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和三角形中位线性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.已知△ABC中,点D在BC边上,且DC=6、S△ADC=15、∠B=45°,△ABD是等腰三角形,则S△ABD=$\frac{25}{2}$或$\frac{25\sqrt{2}}{2}$或25.
11.已知$\frac{1}{x}-\frac{1}{y}=2$,则$\frac{2}{y^2}+\frac{2y-4x}{{{x^2}y}}$的值是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | 8 | D. | $\frac{1}{8}$ |
15. 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )
 如图,数轴上的点A表示的有理数可能是( )
如图,数轴上的点A表示的有理数可能是( )| A. | -3 | B. | -2 | C. | -2.5 | D. | -3.5 |
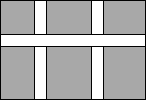 如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽.
如图,要在长100米,宽90米的矩形绿地上,修建三条宽度相同的道路,剩下6块绿地面积共8448平方米,求道路宽. 如图,直线y=2x-3与坐标轴交于A、B两点,交双曲线y=$\frac{k}{x}$于C点,若AB=3BC,则k=2.
如图,直线y=2x-3与坐标轴交于A、B两点,交双曲线y=$\frac{k}{x}$于C点,若AB=3BC,则k=2.