题目内容
16. 如图,直线y=2x-3与坐标轴交于A、B两点,交双曲线y=$\frac{k}{x}$于C点,若AB=3BC,则k=2.
如图,直线y=2x-3与坐标轴交于A、B两点,交双曲线y=$\frac{k}{x}$于C点,若AB=3BC,则k=2.
分析 作辅助线构造相似三角形,利用三角形相似列比例式求得线段的长度,得到点C的坐标,求得k的值.
解答  解:如图在y=2x-3中,令y=0,得x=$\frac{3}{2}$,令x=0,得y=-3,
解:如图在y=2x-3中,令y=0,得x=$\frac{3}{2}$,令x=0,得y=-3,
∴A(0,-3),B($\frac{3}{2}$,0),
∴OA=3,OB=$\frac{3}{2}$,
过点C作CD⊥x轴于D,
∴CD∥OA,
∴△ABO∽△BCD,
∴$\frac{OA}{CD}$=$\frac{OB}{BD}$=$\frac{AB}{BC}$=3,
∴CD=1,BD=$\frac{1}{2}$,
∴C(2,1),
把点C代入y=$\frac{k}{x}$得:k=2,
故答案为:2.
点评 本题主要考查了根据函数的解析式求点的坐标,相似三角形的判定和性质,用待定系数法求比例系数.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
7.下列各数中,有理数是( )
| A. | $\sqrt{5}$ | B. | $\frac{π}{3}$ | ||
| C. | $\frac{1}{2}$ | D. | 3.03003000300003… |
4. 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
 如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )
如图所示,点B在线段AC上,且BC=2AB,点D,E分别是AB,BC的中点,则下列结论错误的是( )| A. | AB=$\frac{1}{3}$AC | B. | EC=2BD | C. | B是AE的中点 | D. | DE=$\frac{2}{3}$AB |
8.比较2$\sqrt{2}$,3,$\sqrt{7}$的大小,正确的是( )
| A. | $\sqrt{7}$<3<2$\sqrt{2}$ | B. | 2$\sqrt{2}$<$\sqrt{7}$<3 | C. | $\sqrt{7}$<2$\sqrt{2}$<3 | D. | 2$\sqrt{2}$<3<$\sqrt{7}$ |
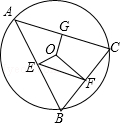 如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.
如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.