题目内容
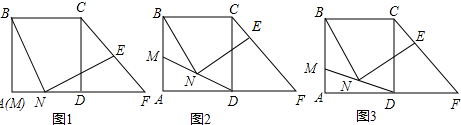
17.已知△ABC中,点D在BC边上,且DC=6、S△ADC=15、∠B=45°,△ABD是等腰三角形,则S△ABD=$\frac{25}{2}$或$\frac{25\sqrt{2}}{2}$或25.分析 先根据三角形面积公式得到△ACD中,DC边上的高,再分三种情况:①AD=BD;②BA=BD;③AB=AD;进行讨论即可求解.
解答 解:△ACD中,DC边上的高为15×2÷6=5,
①AD=BD,如图1所示: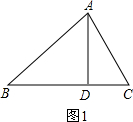
AD=BD=5,
S△ABD=5×5÷2=$\frac{25}{2}$;
②BA=BD,如图2所示: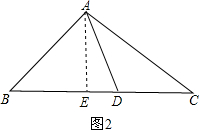
BD=AB=5×$\sqrt{2}$=5$\sqrt{2}$,
S△ABD=5$\sqrt{2}$×5÷2=$\frac{25\sqrt{2}}{2}$;
③AB=AD,如图3所示: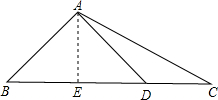
BD=5×2=10,
S△ABD=10×5÷2=25.
故答案为:$\frac{25}{2}$或$\frac{25\sqrt{2}}{2}$或25.
点评 考查了等腰三角形的性质,三角形面积,关键是分类思想的应用,有一定的难度.

练习册系列答案
相关题目
12.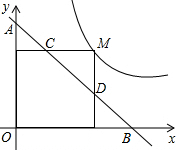 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
 如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )
如图,M为双曲线y=$\frac{{\sqrt{3}}}{x}$上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为( )| A. | $2\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $2\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
7.下列各数中,有理数是( )
| A. | $\sqrt{5}$ | B. | $\frac{π}{3}$ | ||
| C. | $\frac{1}{2}$ | D. | 3.03003000300003… |
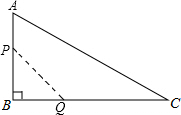 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向B以2mm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以4mm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.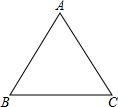 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.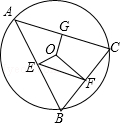 如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.
如图,⊙O的半径是3,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF.若OG﹦1,则EF为2$\sqrt{2}$.