题目内容
10.已知关于x的二次三项式mx2-2(m+2)x+(m+5)在实数范围内不能分解因式,试判断方程(m-5)x2-2(m+2)x+m=0根的情况.分析 由关于x的二次三项式mx2-2(m+2)x+(m+5)在实数范围内不能分解因式,得到方程mx2-2(m+2)x+(m+5)=0无实数根,根据△1=4(m+2)2-4m(m+5)=-4m+16<0,得到m>4,根据△2=4(m+2)2-4m(m-5)=36m+16>0,于是得到方程(m-5)x2-2(m+2)x+m=0有两个不相等的实数根.
解答 解:∵关于x的二次三项式mx2-2(m+2)x+(m+5)在实数范围内不能分解因式,
∴mx2-2(m+2)x+(m+5)=0无实数根,
∴△1=4(m+2)2-4m(m+5)=-4m+16<0,
∴m>4,
∵△2=4(m+2)2-4m(m-5)=36m+16,
∵m>4,
∴△2=36m+16>0,
∴方程(m-5)x2-2(m+2)x+m=0有两个不相等的实数根.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 已知:如图△ABC中,CD是∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE的长.
已知:如图△ABC中,CD是∠ACB平分线,DE∥BC,AD:DB=2:3,AC=a,求DE的长.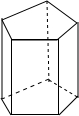 如图所示的是一个五棱柱.它的底面边长都是4cm.侧棱长都是6cm.
如图所示的是一个五棱柱.它的底面边长都是4cm.侧棱长都是6cm.