题目内容
9.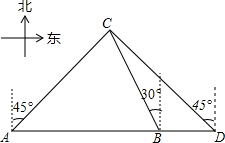 如图,某轮船由西向东方向航行,在A处望见灯塔C在东北方向,航行到点B处望见灯塔C在北偏西30°方向,又航行了半小时到达D处,望见灯塔C恰好在西北方向,若轮船的速度为40海里/时,求A,B之间的距离(精确到0.1海里).
如图,某轮船由西向东方向航行,在A处望见灯塔C在东北方向,航行到点B处望见灯塔C在北偏西30°方向,又航行了半小时到达D处,望见灯塔C恰好在西北方向,若轮船的速度为40海里/时,求A,B之间的距离(精确到0.1海里).
分析 先作CE⊥AD,根据BD=20,AE=DE,可求AE、CE的长,通过解直角△CEB得到BE的长度,从而求得AB的长.
解答 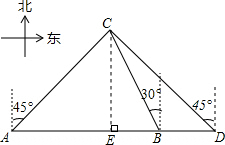 解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=$\frac{\sqrt{3}}{3}$x,
解:作CE⊥AD于点E,设AE=x,则CE=AE=x,BE=$\frac{\sqrt{3}}{3}$x,
∵BD=20,AE=DE,
∴x=$\frac{\sqrt{3}}{3}$x+20,
∴x=30+10$\sqrt{3}$,$\frac{\sqrt{3}}{3}$x=10+10$\sqrt{3}$,
则AB=AE+BE=x+$\frac{\sqrt{3}}{3}$x=40+20$\sqrt{3}$≈74.6(海里).
答A,B之间的距离约为74.6海里.
点评 本题考查了方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,关键是作出辅助线,构造直角三角形.

练习册系列答案
相关题目
14.方程x2-2x-5=0经配方后,可化为( )
| A. | (x-1)2=6 | B. | (x+1)2=6 | C. | (x-1)2=4 | D. | (x+1)2=4 |
 如图,矩形ABCD的面积为48,其中一边AB的长为6,求矩形的对角线长.
如图,矩形ABCD的面积为48,其中一边AB的长为6,求矩形的对角线长.