题目内容
10. 在锐角△ABC中,D、E、F分别是三条高AD、BE、CF.的垂足,连DE、EF、FD,求证:△DEC∽△AEF∽△DBF.
在锐角△ABC中,D、E、F分别是三条高AD、BE、CF.的垂足,连DE、EF、FD,求证:△DEC∽△AEF∽△DBF.
分析 先根据有两组角对应相等的两个三角形相似判断△ABE∽△ACF,得到$\frac{AE}{AF}$=$\frac{AB}{AC}$,则利用比例性质得$\frac{AE}{AB}$=$\frac{AF}{AC}$,加上∠EAF=∠BAC,于是可根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△AEF∽△ABC,利用同样方法可得△DEC∽△ABC,△DBF∽△ABC,然后利用相似的传递性可得结论.
解答 证明:∵BE和CF为高,
∴∠AEB=∠AFC=90°,
而∠BAE=∠CAF,
∴△ABE∽△ACF,
∴$\frac{AE}{AF}$=$\frac{AB}{AC}$,
∴$\frac{AE}{AB}$=$\frac{AF}{AC}$,
而∠EAF=∠BAC,
∴△AEF∽△ABC,
同理可得△DEC∽△ABC,△DBF∽△ABC,
∴△DEC∽△AEF∽△DBF.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.也考查了相似三角形的性质.

练习册系列答案
相关题目
 如图,
如图,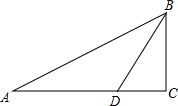 如图,在Rt△ABC中,∠C=90°,BD是∠ABC平分线,BD=10$\sqrt{6}$,BC=15$\sqrt{2}$.求AB和AD的长.
如图,在Rt△ABC中,∠C=90°,BD是∠ABC平分线,BD=10$\sqrt{6}$,BC=15$\sqrt{2}$.求AB和AD的长.