题目内容
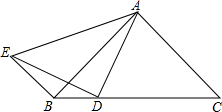 △ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.
△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:根据AB=AC,可得∠C与∠ABC的关系,根据BE∥AC,可得∠C与∠DBM的关系,根据角平分线的性质,可得DM与DN的关系,根据HL,可得△AND与△EMD的关系,根据三角形全等,可得证明结果.
解答:证明:如图,做DN⊥AB,DM⊥BE,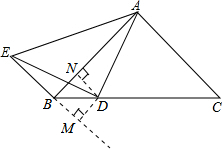 ,
,
∵AB=AC,
∴∠ABC=∠C(等边对等角).
∵BE∥AC,
∴∠C=∠DBM(两直线平行,内错角相等).
∴∠NBD=∠MBD(等量代换).
∵DN⊥AB,DM⊥BE,
∴DM=DN(角平分线上的点到角两边的距离相等).
在△AND和△EMD中,
∴Rt△AND≌Rt△EMD(HL),
∠DAB=∠BED(全等三角形的对应角相等).
 ,
,∵AB=AC,
∴∠ABC=∠C(等边对等角).
∵BE∥AC,
∴∠C=∠DBM(两直线平行,内错角相等).
∴∠NBD=∠MBD(等量代换).
∵DN⊥AB,DM⊥BE,
∴DM=DN(角平分线上的点到角两边的距离相等).
在△AND和△EMD中,
|
∴Rt△AND≌Rt△EMD(HL),
∠DAB=∠BED(全等三角形的对应角相等).
点评:本题考查了全等三角形的判定与性质,先证明DN=DM,再证明△AND≌△EMD,最后证明角相等.

练习册系列答案
相关题目
 如图直线y=x+2与双曲线y=
如图直线y=x+2与双曲线y=| m-3 |
| x |
| A、m>2 | B、2<m<3 |
| C、m<3 | D、m>3或m<2 |
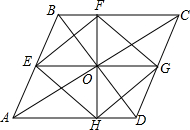 过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由.
过平行四边形ABCD的对角线AC的中点O作两条互相垂直的直线,分别交AB,BC,CD,DA于E,F,G,H四点,连接EF,FG,GH,HE.试判断四边形EFGH的形状,并说明理由. 如图,等腰△ABC,其中AB=BC,AB比AC长12cm,若△ABC的周长为96cm,求AC的长.
如图,等腰△ABC,其中AB=BC,AB比AC长12cm,若△ABC的周长为96cm,求AC的长.