题目内容
 如图,已知点B的坐标为(6,0),点P的坐标为(4,-4),在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由.
如图,已知点B的坐标为(6,0),点P的坐标为(4,-4),在直线y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由.考点:一次函数综合题
专题:
分析:作AB⊥直线y=2x于点A,PE⊥直线y=2x于点E,作DF⊥OB于F,设AB的解析式为y=kx+b,由待定系数法就可以AB的解析式,进而可以求出PE的解析式,就可以求出A、P的坐标,由等腰梯形的性质就可以得出PO=BD,PB∥AE,就可以得出AB=PE,由三角形全等就可以得出OE=AD,由两点间的距离公式就可以求出OE,BP的值,就可以求出OD的值,作DF⊥OB于点F,设D(m,2m),由勾股定理就可以求出m的值,进而求出结论.
解答:解:AB⊥直线y=2x于点A,PE⊥直线y=2x于点E,作DF⊥OB于F,
∴∠BAE=∠AEP=90°.AB∥BP.
设直线AB的解析式为y=k1x+b1,由题意,得
,
解得:
,
∴直线AB的解析式为:y=-
x+3.
设PE的解析式为y=k2x+b2,由题意,得
,
解得:
,
∴直线PE的解析式为:y=-
x-2.
设PB的解析式为y=k3x+b3,由题意,得
,
解得:
,
∴直线AB的解析式为:y=2x-12.
∵直线AE的解析式为y=2x,
∴AE∥BP,
∵AB∥BP.
∴四边形AEPB是平行四边形,
∵∠AEP=90°,
∴平行四边形AEPB是矩形,
∴PE=BA.AE=BP.
∵四边形PBDO是等腰梯形,
∴PO=BD.
在Rt△PEO和Rt△BDA中,
,
∴Rt△PEO≌Rt△BDA(HL),
∴OE=DA.
∵
,
解得:
,
∴E(-
,-
),
∴OE=
.
∴DA=
.
∵BP=
=2
,
∴AE=2
,
∴OD=2
-2×
=
.
设D(m,2m),作DF⊥OB于点F.
∴OF=m,DF=2m.
在Rt△DOF中,由勾股定理,得
m2+4m2=
解得:m=±
.
∵点D在第一象限,
∴m>0,
∴m=
.
∴DF=
,
∴D(
,
).
∴∠BAE=∠AEP=90°.AB∥BP.
设直线AB的解析式为y=k1x+b1,由题意,得
|
解得:
|
∴直线AB的解析式为:y=-
| 1 |
| 2 |
设PE的解析式为y=k2x+b2,由题意,得
|
解得:
|
∴直线PE的解析式为:y=-
| 1 |
| 2 |
设PB的解析式为y=k3x+b3,由题意,得
|
解得:
|
∴直线AB的解析式为:y=2x-12.
∵直线AE的解析式为y=2x,
∴AE∥BP,
∵AB∥BP.
∴四边形AEPB是平行四边形,
∵∠AEP=90°,
∴平行四边形AEPB是矩形,
∴PE=BA.AE=BP.
∵四边形PBDO是等腰梯形,
∴PO=BD.
在Rt△PEO和Rt△BDA中,
|
∴Rt△PEO≌Rt△BDA(HL),
∴OE=DA.
∵
|

解得:
|
∴E(-
| 4 |
| 5 |
| 8 |
| 5 |
∴OE=
4
| ||
| 5 |
∴DA=
4
| ||
| 5 |
∵BP=
| (6-4)2+(0+4)2 |
| 5 |
∴AE=2
| 5 |
∴OD=2
| 5 |
4
| ||
| 5 |
2
| ||
| 5 |
设D(m,2m),作DF⊥OB于点F.
∴OF=m,DF=2m.
在Rt△DOF中,由勾股定理,得
m2+4m2=
| 4 |
| 5 |
解得:m=±
| 2 |
| 5 |
∵点D在第一象限,
∴m>0,
∴m=
| 2 |
| 5 |
∴DF=
| 4 |
| 5 |
∴D(
| 2 |
| 5 |
| 4 |
| 5 |
点评:本题考查了垂线的性质的运用,等腰梯形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,一次函数的解析式的运用,平面上两点间的距离公式的运用,一次函数与二元一次方程组的关系的运用,解答时求出函数的解析式是关键.

练习册系列答案
相关题目
一元二次方程x(x-2014)=2014-x的根是( )
| A、-1 | B、2014 |
| C、1和2014 | D、-1和2014 |
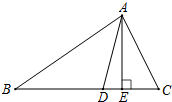 如图,AD、AE分别是△ABC的角平分线和高.
如图,AD、AE分别是△ABC的角平分线和高. 如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠BDC的度数为
如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠BDC的度数为