题目内容
5.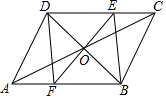 在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )
| A. | 小青 | B. | 小荷 | C. | 小夏 | D. | 小雨 |
分析 利用平行四边形的性质、全等三角形的判定和性质,一一判断即可.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC,CD∥AB,
∴∠ECO=∠FAO,(故小雨的结论正确),
在△EOC和FOA中,
$\left\{\begin{array}{l}{∠EOC=∠AOF}\\{∠ECO=∠OAF}\\{OC=OA}\end{array}\right.$,
∴△EOC≌△FOA,
∴OE=OF(故小青的结论正确),
∴S△EOC=S△AOF,
∴S四边形AFED=S△ADC=$\frac{1}{2}$S平行四边形ABCD,
∴S四边形AFED=S四边形FBCE故小夏的结论正确,
∵△EOC≌△FOA,
∴EC=AF,∵CD=AB,
∴DE=FB,DE∥FB,
∴四边形DFBE是平行四边形,
∵OD=OB,EO⊥DB,
∴ED=EB,
∴四边形DFBE是菱形,无法判断是正方形,故小何的结论错误,
故选B.
点评 本题考查平行四边形的性质、全等三角形的判定和性质、线段的垂直平分线的性质正方形的判定、菱形的判定等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
17.下列命题是真命题的是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 同旁内角互补 | |
| C. | 若a2=b2,则|a|=|b| | |
| D. | 若a>0,则a2>a |
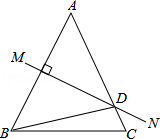 如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°.
如图,等腰△ABC中,AB=AC,∠BAC=50°,AB的垂直平分线MN交AC于点D,则∠DBC的度数是15°. 如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=80°.
如图,点D、E分别是△ABC的边AC、BC上的点,AD=DE,AB=BE,∠A=80°,则∠BED=80°. 如图,在五边形ABCDE中,若∠1+∠2+∠3+∠4=280°,则∠D=100°.
如图,在五边形ABCDE中,若∠1+∠2+∠3+∠4=280°,则∠D=100°. 如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.
如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD.