题目内容
 如图,在六边形ABCDEF中,所有角都相等.
如图,在六边形ABCDEF中,所有角都相等.(1)求各内角的度数;
(2)分别向两侧延长EF、AB、CD,且两两相交于交于点G、H、P,试探索△GHP有什么特征,并说明理由;
(3)试判断六边形ABCDEF的对边有什么位置关系,并说明理由.
考点:等边三角形的判定与性质,平行线的判定,多边形内角与外角
专题:
分析:(1)先求出六边形内角和=720°,即可求出每个内角为120°;
(2)由∠GFA=∠GAF=60°,得出∠G=60,∠P=∠H=60°,证出△GHP是等边三角形;
(3)根据平行线的判定方法由∠DEF+∠G=180°,证出DE∥AB,同理得出 EF∥BC,AF∥CD.
(2)由∠GFA=∠GAF=60°,得出∠G=60,∠P=∠H=60°,证出△GHP是等边三角形;
(3)根据平行线的判定方法由∠DEF+∠G=180°,证出DE∥AB,同理得出 EF∥BC,AF∥CD.
解答:解:(1)∵六边形内角和为(6-2)•180°=720°,六个角相等,
∴∠EFA=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°;
(2)△GHP是等边三角形;如图所示:
由(1)可知∠GFA=∠GAF=60°,
∴∠G=60°,
同理∠P=∠H=60°,
∴△GHP是等边三角形;
(3)六边形ABCDEF的对边平行;理由如下:
∵∠DEF+∠G=180°,
∴DE∥AB,
同理 EF∥BC,AF∥CD.
∴∠EFA=∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=120°;
(2)△GHP是等边三角形;如图所示:

由(1)可知∠GFA=∠GAF=60°,
∴∠G=60°,
同理∠P=∠H=60°,
∴△GHP是等边三角形;
(3)六边形ABCDEF的对边平行;理由如下:
∵∠DEF+∠G=180°,
∴DE∥AB,
同理 EF∥BC,AF∥CD.
点评:本题考查了多边形的内角和、等边三角形的判定与性质以及平行线的判定;根据内角和求出各个角的度数以及运用定理推理计算是解决问题的关键.

练习册系列答案
相关题目
关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为( )
A、x<
| ||
| B、x≠1的实数 | ||
C、
| ||
| D、以上都不对 |
 如图,当风车的一片叶子AB旋转到与地面MN平行时,叶子CD与地面MN
如图,当风车的一片叶子AB旋转到与地面MN平行时,叶子CD与地面MN 如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.
如图,直线AB,CD相交于点O,OE平分∠BOC,FO⊥CD于点O,若∠BOD:∠EOB=2:3,求∠AOF的度数.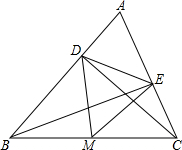 已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.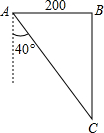 如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)
如图,东西两炮台A、B相距2000米,同时发现入侵舰C,炮台A测得敌舰C在它的南偏东40°的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离分别是多少米?(精确到1米)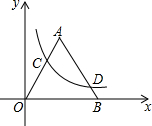 如图,△AOB是边长为a的等边三角形,OC=3BD,求反比例函数y=
如图,△AOB是边长为a的等边三角形,OC=3BD,求反比例函数y=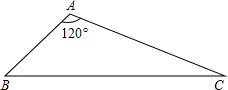 如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC.
如图,AB=2,AC=4,∠BAC=120°,求BC及S△ABC. 如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.
如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.