题目内容
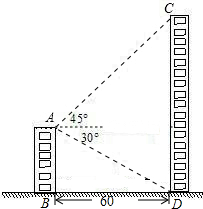 如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).
如图,小明在顶楼A处测得对面大楼楼顶点C处的仰角为45°,楼底点D处的俯角为30°,若两座楼AB与CD相距60米,求楼CD的高度约为多少米(结果保留三个有效数字).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:在题中两个直角三角形中,知道已知角和其邻边,只需根据正切值求出对边后相加即可.
解答: 解:过点A的水平线交CD于点E,则AE⊥CD,
解:过点A的水平线交CD于点E,则AE⊥CD,
∵四边形ABDE是矩形,
∴AE=BD=60.
∵∠CAE=45°,
∴△AEC是等腰直角三角形,
∴CE=AE=60,
在Rt△AED中,tan∠EAD=
,
∴ED=60×tan30°=60×
=20
,
∴CD=CE+ED=60+20
.
答:楼CD的高是(60+20
)米.
 解:过点A的水平线交CD于点E,则AE⊥CD,
解:过点A的水平线交CD于点E,则AE⊥CD,∵四边形ABDE是矩形,
∴AE=BD=60.
∵∠CAE=45°,
∴△AEC是等腰直角三角形,
∴CE=AE=60,
在Rt△AED中,tan∠EAD=
| ED |
| AE |
∴ED=60×tan30°=60×
| ||
| 3 |
| 3 |
∴CD=CE+ED=60+20
| 3 |
答:楼CD的高是(60+20
| 3 |
点评:本题考查的解直角三角形的应用-仰角俯角问题,此类题目要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
关于x的不等式ax2-(a2+1)x+a>0(a≠0)的解集为( )
A、x<
| ||
| B、x≠1的实数 | ||
C、
| ||
| D、以上都不对 |
 如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径.
如图,P是⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径. 如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.
如图,在△ABC中,中位线EF与中线AD相交于点O.求证:AD与EF互相平分.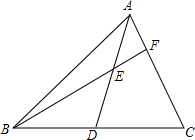 如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=
如图,AD是△ABC的中线,E是AD的中点,F是BE延长线与AC的交点,求证:AF=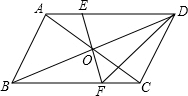 如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
如图,AC、BD为?ABCD的对角线,O为两条对角线的交点,过点O作EF⊥BD,与AD、BC分别交于点E、F,试猜想DE与DF之间的关系,并说明理由.
 如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.