题目内容
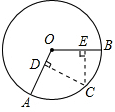如图，点C是 |
| AB |
|
| AB |
考点：圆心角、弧、弦的关系,角平分线的性质
专题：证明题
分析：先利用角平分线的性质定理得到OC平分∠AOB，则∠AOC=∠BOC，然后根据圆心角、弧、弦的关系即可得到结论．
解答：证明：连结OC，如图，
∵CD⊥OA于D，CE⊥OB于E，CD=CE，
∴OC平分∠AOB，
∴∠AOC=∠BOC，
∴
=
，
即点C是
的中点．
∵CD⊥OA于D，CE⊥OB于E，CD=CE，
∴OC平分∠AOB，
∴∠AOC=∠BOC，
∴
|
| AC |
|
| BC |
即点C是
|
| AB |
点评：本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了角平分线的性质．
练习册系列答案
阅读快车系列答案
相关题目
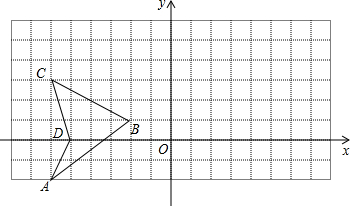
如图，当风车的一片叶子AB旋转到与地面MN平行时，叶子CD与地面MN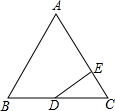
如图，△ABC是等边三角形，D为BC边的中点，DE⊥AC于点E．试探索线段CE与线段AC的数量关系，并说明理由．
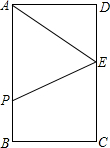如图，矩形ABCD中，AB=12cm，BC=8cm，E为CD的中点．点P从A点出发，沿A-B-C的方向在矩形边上匀速运动，速度为1cm/s，运动到C点停止．设点P运动的时间为ts．
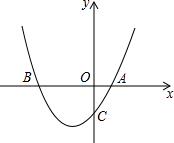如图，已知二次函数y=ax2+bx+c经过点A（1，0），C（0，3），且对称轴为直线x=-1．
如图，直线AB，CD相交于点O，OE平分∠BOC，FO⊥CD于点O，若∠BOD：∠EOB=2：3，求∠AOF的度数．关于x的不等式ax2-（a2+1）x+a＞0（a≠0）的解集为（ ）
A、x＜
| ||
| B、x≠1的实数 | ||
C、
| ||
| D、以上都不对 |