题目内容
11.计算:(1)$\frac{1}{x-3}$-$\frac{3}{x(x-3)}$
(2)($\frac{m}{m+3}$-$\frac{2m}{m+3}$)÷$\frac{m}{{m}^{2}-9}$
(3)|-2|+($\frac{1}{3}$)2+(π-2)0-$\sqrt{9}$.
分析 (1)先对原式通分变为同分母分式,然后化简即可解答本题;
(2)先对括号内的式子化简,再根据分式的除法进行计算即可解答本题;
(3)根据绝对值、负整数指数幂、零指数幂、算术平方根可以对原式化简,然后合并同类项即可解答本题.
解答 解:(1)$\frac{1}{x-3}$-$\frac{3}{x(x-3)}$
=$\frac{x-3}{x(x-3)}$
=$\frac{1}{x}$;
(2)($\frac{m}{m+3}$-$\frac{2m}{m+3}$)÷$\frac{m}{{m}^{2}-9}$
=$\frac{m-2m}{m+3}×\frac{(m+3)(m-3)}{m}$
=$\frac{-m}{m+3}×\frac{(m+3)(m-3)}{m}$
=3-m;
(3)|-2|+($\frac{1}{3}$)2+(π-2)0-$\sqrt{9}$
=2+$\frac{1}{9}+1-3$
=$\frac{1}{9}$.
点评 本题考查分式的混合运算、实数的运算、零指数幂、负整数指数幂,解题的关键是明确它们各自的计算方法.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
6.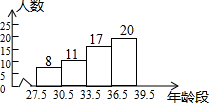 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
 菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )
菲尔兹奖(Fields Medal)是享有崇高声誉的数学大奖,每四年颁奖一次,颁给二至四名成就显著的年轻数学家,下面是对截至2015年56名获奖者的年龄进行统计得到的统计图.则下列说法中正确的是( )| A. | 平均年龄是37.5岁 | B. | 中位数年龄位于33.5-36.5岁 | ||
| C. | 众数年龄位于36.5-39.5岁 | D. | 以上选项都不正确 |
3.实数$\sqrt{5}$的值在( )
| A. | 0与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
 如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.
如图(1),AB∥CD,猜想∠BPD与∠B、∠D的数量关系,并说明理由.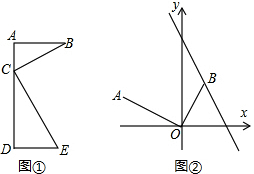 探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):
探究与应用:在学习几何时,我们可以通过分离和构造基本图形,将几何“模块”化.例如在相似三角形中,K字形是非常重要的基本图形,可以建立如下的“模块”(如图①):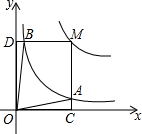 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论: 有理数a、b在数轴上的位置如图所示,那么a+b<0(填“>”、“<”或“=”)
有理数a、b在数轴上的位置如图所示,那么a+b<0(填“>”、“<”或“=”)