题目内容
10．某学习小组设计了一个摸球试验，在袋中装有黑，白两种颜色的球，这些球的形状大小质地等完全相同，即除颜色外无其他差别．在看不到球的情况下，随机从袋中摸出一个球，记下颜色，再把它放回，不断重复．下表是由试验得到的一组统计数据：| 摸球的次数 | 100 | 200 | 300 | 400 | 500 | 600 |
| 摸到白球的次数 | 58 | 118 | 189 | 237 | 302 | 359 |
| 摸到白球的频率 | 0.58 | 0.59 | 0.63 | 0.593 | 0.604 | 0.598 |
分析 用所有频率的平均数即可表示事件发生的概率．
解答 解：是白球的概率为：$\frac{0.58+0.59+0.63+0.593+0.598}{5}$=0.6，
故答案为：0.6．
点评 本题考查了利用频率估计概率的知识，解题的关键是了解大量重复试验中，事件发生的频率可以估计概率．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
20．下列等式由左边到右边的变形中，属于因式分解的是（ ）
| A． | （a+1）（a-1）=a2-1 | B． | a2-6a+9=（a-3）2 | ||
| C． | x2+2x+1=x（x+2）+1 | D． | -18x4y3=-6x2y2•3x2y |
1．
把一张对边互相平行的纸条，折成如图所示，EF是折痕，若∠EFB=32°，那么∠AEG的度数是（ ）
把一张对边互相平行的纸条，折成如图所示，EF是折痕，若∠EFB=32°，那么∠AEG的度数是（ ）| A． | 148° | B． | 64° | C． | 116° | D． | 136° |
18．
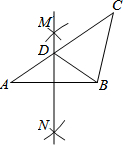在△ABC中，按以下步骤作图：①分别以A，B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若CD=BC，∠A=35°，则∠C=（ ）
在△ABC中，按以下步骤作图：①分别以A，B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若CD=BC，∠A=35°，则∠C=（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
5．
如图是某几何体的三视图，该几何体是（ ）
如图是某几何体的三视图，该几何体是（ ）| A． | 三棱柱 | B． | 三棱锥 | C． | 长方体 | D． | 正方体 |
2．在五张完全相同的卡片上，分别写有数字0，-1，-2，1，3，现从中随机抽取一张，抽到写有负数的卡片的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{5}$ |
19．函数$y=\frac{1}{{\sqrt{x-1}}}$中自变量的取值范围是（ ）
| A． | x≠1 | B． | x＞1 | C． | x≥1 | D． | x≥-1 |
