题目内容
15.已知关于x的方程kx2-x-$\frac{2}{k}$=0(k≠0).(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根都是整数,求整数k的值.
分析 (1)先判断方程为关于x的一元二次方程,再计算出△=9,于是根据判别式的意义可判断方程总有两个不相等的实数根;
(2)利用求根公式解方程得到x1=$\frac{2}{k}$,x2=-$\frac{1}{k}$,然后利用整数的整除性确定k的值.
解答 (1)证明:∵k≠0,
∴kx2-x-$\frac{2}{k}$=0(k≠0)为关于x的一元二次方程,
∵△=(-1)2-4k×(-$\frac{2}{k}$)=9>0,
∴方程总有两个不相等的实数根;
(2)解:x=$\frac{1±\sqrt{9}}{2k}$=$\frac{1±3}{2k}$,解得x1=$\frac{2}{k}$,x2=-$\frac{1}{k}$,
∵方程的两个实数根都是整数,且k是整数,
∴k=-1或k=1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
10.某学习小组设计了一个摸球试验,在袋中装有黑,白两种颜色的球,这些球的形状大小质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋中摸出一个球,记下颜色,再把它放回,不断重复.下表是由试验得到的一组统计数据:
从这个袋中随机摸出一个球,是白球的概率约为0.6.(结果精确到0.1)
| 摸球的次数 | 100 | 200 | 300 | 400 | 500 | 600 |
| 摸到白球的次数 | 58 | 118 | 189 | 237 | 302 | 359 |
| 摸到白球的频率 | 0.58 | 0.59 | 0.63 | 0.593 | 0.604 | 0.598 |
7. 如图是某一正方体的展开图,那么该正方体是( )
如图是某一正方体的展开图,那么该正方体是( )
 如图是某一正方体的展开图,那么该正方体是( )
如图是某一正方体的展开图,那么该正方体是( )| A. |  | B. |  | C. |  | D. |  |
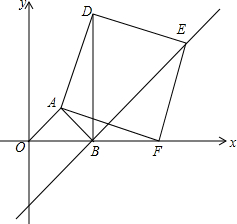 如图,正方形OABC的顶点A在第一象限,B点坐标为(2,0),正方形ADEF顶点F坐标为(4,0).
如图,正方形OABC的顶点A在第一象限,B点坐标为(2,0),正方形ADEF顶点F坐标为(4,0).