题目内容
1. 把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )
把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,那么∠AEG的度数是( )| A. | 148° | B. | 64° | C. | 116° | D. | 136° |
分析 先根据图形折叠的性质求出∠C′EF=∠CEF,再根据平行线的性质得出∠CEF的度数,由补角的定义即可得出结论.
解答 解:∵∠CEF由∠C′EF折叠而成,
∴∠CEF=∠C′EF,
∵AC′∥BD′,∠EFB=32°,
∴∠C′EF=∠EFB=32°,
∴∠AG=180°-32°-32°=116°.
故选C.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.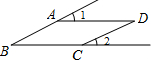 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )
 如图,∠1=∠B,∠2=25°,则∠D=( )
如图,∠1=∠B,∠2=25°,则∠D=( )| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
10.某学习小组设计了一个摸球试验,在袋中装有黑,白两种颜色的球,这些球的形状大小质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋中摸出一个球,记下颜色,再把它放回,不断重复.下表是由试验得到的一组统计数据:
从这个袋中随机摸出一个球,是白球的概率约为0.6.(结果精确到0.1)
| 摸球的次数 | 100 | 200 | 300 | 400 | 500 | 600 |
| 摸到白球的次数 | 58 | 118 | 189 | 237 | 302 | 359 |
| 摸到白球的频率 | 0.58 | 0.59 | 0.63 | 0.593 | 0.604 | 0.598 |
11.已知a、b、c为非零实数,且满足$\frac{b+c}{a}=\frac{a+b}{c}=\frac{a+c}{b}=k$,则一次函数y=kx+k+1的图象一定经过( )
| A. | 第一、二、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 第二象限 |
 已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形.
已知:如图,矩形ABCD的对角线AB、BD相交于点O,DE∥CA,AE∥BD.求证:四边形AODE是菱形. 已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.
已知如图,O是△ABC内一点,求证:∠AOB=∠1+∠2+∠C.