题目内容
4.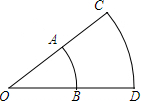 如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
分析 设∠O=n°,由弧长公式和已知条件得$\frac{nπ}{180}$(OC-OA)=$\frac{2}{3}π$,即$\frac{nπ}{180}×2$=$\frac{2}{3}π$,得出n=60,因此∠O=60°,再由弧长公式得出$\frac{60π×OA}{180}=π$,即可得出OA的长.
解答 解:设∠O=n°,
∵$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,
∴$\frac{nπ×OA}{180}$=π,$\frac{nπ×OC}{180}$=$\frac{5}{3}π$,
∴$\frac{nπ×OC}{180}-\frac{nπ×OA}{180}$=$\frac{5}{3}π$-π,
∴$\frac{nπ}{180}$(OC-OA)=$\frac{2}{3}π$,
即$\frac{nπ}{180}×2$=$\frac{2}{3}π$,
解得:n=60,
∴∠O=60°,
∵$\frac{60π×OA}{180}=π$,
解得:OA=3.
点评 本题考查了弧长公式;灵活运用弧长公式,根据题意求出∠O的度数是解决问题的关键.

练习册系列答案
相关题目
14.下列图形是轴对称而不是中心对称图形的是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 等边三角形 |
9.已知点A(0,2),B(2,0),点C在y=x2的图象上,若△ABC的面积为$\frac{9}{4}$,则这样的C点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6.
如图,已知∠AOB等于30°,角内有一点P,OP=6,点M在OA上,点N在OB上,△PMN周长的最小值是6.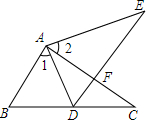 如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
如图所示,点E在△ABC外部,点D在BC边上.DE交AC于F,若∠1=∠2,∠E=∠C,AE=AC,求证:△ABC≌△ADE.