题目内容
9.已知点A(0,2),B(2,0),点C在y=x2的图象上,若△ABC的面积为$\frac{9}{4}$,则这样的C点有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据二次函数图象上点的坐标特征,设C(t,t2),利用S四边形AOBC=S△AOB+S△ABC=S△AOC+S△OBC,得到$\frac{1}{2}$×2×|t|+$\frac{1}{2}$×2×t2=$\frac{1}{2}$×2×2+$\frac{9}{4}$,整理得t2+|t|=$\frac{17}{4}$,然后去绝对值解方程可判断C点的个数.
解答 解:设C(t,t2),
∵S四边形AOBC=S△AOB+S△ABC=S△AOC+S△OBC,
∴$\frac{1}{2}$×2×|t|+$\frac{1}{2}$×2×t2=$\frac{1}{2}$×2×2+$\frac{9}{4}$,
整理得t2+|t|=$\frac{17}{4}$,
当t>0时,t2+t=$\frac{17}{4}$,解得t1=$\frac{-1+3\sqrt{2}}{2}$,t2=$\frac{-1-3\sqrt{2}}{2}$(舍去),
当t<0时,t2-t=$\frac{17}{4}$,解得t1=$\frac{1+3\sqrt{2}}{2}$(舍去),t2=$\frac{1-3\sqrt{2}}{2}$,
∴t的值为$\frac{-1+3\sqrt{2}}{2}$和$\frac{1+3\sqrt{2}}{2}$,即这样的C点有2个.
故选B.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足二次函数的解析式.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
1.某公园的门票价格规定如下表:实验中学组织七年级两个班到这个公园郊游,两班共有学生104人,其中(一)班不足50人,(二)班多于50人,购买门票时,若两个班各自统一购票,则需1136元;若两个班合在一起购票,就可以节省一部分钱.
(1)两班各有学生多少人?
(2)两个班合在一起购票比两个班各自统一购票分别节省多少钱?
| 购票人数/人 | 1~50 | 51~100 | 100以上 |
| 每人票价/元 | 12 | 10 | 8 |
(2)两个班合在一起购票比两个班各自统一购票分别节省多少钱?
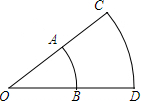 如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.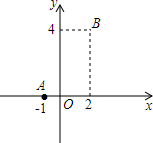 如图,在平面直角坐标系中,已知点A(-1,0),B(2,4),试求x轴上确定点C,使AC=AB,并求点C的坐标.
如图,在平面直角坐标系中,已知点A(-1,0),B(2,4),试求x轴上确定点C,使AC=AB,并求点C的坐标.