题目内容
14.已知一次函数y=(3-k)x-2k2+18.(1)当k=-3时,其图象经过原点;
(2)当k>3时,y随x的增大而减小;
(3)当-3<k<3时,其图象与y轴的交点在x轴的上方;
(4)当k=4时.其图象平行于直线y=-x.
分析 (1)把原点代入解析式,即可求得k的值;
(2)根据函数图象性质,知系数3-k<0,即可求得k的取值;
(3)根据函数图象性质,知-2k2+18>0,即可求得k的取值;
(4)根据平行的性质,知3-k=-1,即可求得k的值.
解答 解:(1)把(0,0)代入解析式得:-2k2+18=0,
解得:k=±3,又3-k≠0,
所以k=-3;
(2)∵y随x的增大而减小,
∴3-k<0,即k>3;
(3)∵图象与y轴的交点在x轴的上方,
∴-2k2+18>0,
解得-3<k<3;
(4)∵图象平行于直线y=-x,
∴3-k=-1,即k=4,
故答案为:-3;<3;-3<k<3;4.
点评 本题考查了一次函数图象上点的坐标特征及函数性质,是基础题型,熟练掌握一次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列说法正确的是( )
| A. | 整式一定是单项式 | |
| B. | 多项式22x2+ab2是4次二项式 | |
| C. | 多项式a2-3x+4y-(a2-3x+4y)的值与a、x、y的值无关 | |
| D. | 多项式x2+2y2的系数是2 |
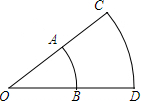 如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长.
如图,$\widehat{AB}$和$\widehat{CD}$都是以O为圆心的弧,$\widehat{AB}$的长为π,$\widehat{CD}$的长为$\frac{5}{3}$π,BD=2,求∠O的度数及OA的长. 如图,已知线段a、b,求作线段AB,使得AB=2b-a(不写作法).
如图,已知线段a、b,求作线段AB,使得AB=2b-a(不写作法). 如图,在平面直角坐标系中,半径为4的⊙O交坐标轴于A、B、C、D,点P为 弧BC上一个点(不与B、C点重合),连结PD.若△PAB的内切圆圆心为G,半径为1,则PD=5$\sqrt{2}$.
如图,在平面直角坐标系中,半径为4的⊙O交坐标轴于A、B、C、D,点P为 弧BC上一个点(不与B、C点重合),连结PD.若△PAB的内切圆圆心为G,半径为1,则PD=5$\sqrt{2}$.