题目内容
5．
如图所示，在四边形ABCD中，AD∥BC，AD⊥DC，AB⊥AC，∠B=60°，CD=$\frac{\sqrt{3}}{2}$cm，求BC的长．
分析 设AB=x，则BC=2x，根据已知及勾股定理列方程，即可求得BC的长．
解答 解：在Rt△ABC中，根据两个锐角互余，得：∠ACB=30°．
∵AD∥BC，
∴∠DAC=∠ACB=30°，
∵AD⊥DC，
∴AC=2CD=$\sqrt{3}$
设AB=x，则BC=2x
根据勾股定理得：4x2-x2=3，
解得x=1，2x=2，
∴BC=2．
点评 重点运用了直角三角形中，30°所对的直角边是斜边的一半．熟练运用勾股定理列方程计算．
练习册系列答案
相关题目
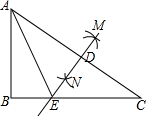如图所示，在Rt△ABC中，∠B=90°，∠C=30°，分别以A、C为圆心，大于$\frac{1}{2}$AC长为半径画弧，两弧相交于点M、N，连接MN，与AC、BC分别交于点D、E，连接AE
在端午节来临之际，某店购进两种品牌的盒装粽子，购进乙品牌盒装粽子的数量y（盒）与甲品牌盒装粽子的数量x（盒）之间的函数关系如图所示：