题目内容
7.在?ABCD中,AB=6,AC=8,则对角线BD的取值范围是4<BD<20.分析 根据题意画出图形,根据平行四边形的对角相互相平分,可得OA=OC,OB=OD;根据三角形的三边关系,可得BD的取值范围.
解答 解:∵四边形ABCD是平行四边形,AC=8,AB=6,
∴OA=OC=$\frac{1}{2}$AC=4,
在△AOB中,
∵AB-OA<OB<AB+OA,
∴2<OB<10,
∵BD=2OB,
∴BD的取值范围是4<BD<20,
故答案为:4<BD<20.
点评 此题考查了平行四边形的性质:平行四边形的对角相互相平分.还考查了三角形的三边关系:三角形中任意两边之和>第三边,三角形中任意两边之差<第三边.题目比较简单,解题时要细心.

练习册系列答案
相关题目
15.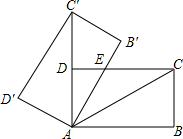 如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
 如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形A′B′C′D′的位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )| A. | 3 | B. | 1.5 | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
2.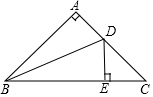 如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,若AB=a,AD=b,则△DCE的周长为( )
如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,若AB=a,AD=b,则△DCE的周长为( )
 如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,若AB=a,AD=b,则△DCE的周长为( )
如图,△ABC是等腰直角三角形,BD平分∠ABC,DE⊥BC于点E,若AB=a,AD=b,则△DCE的周长为( )| A. | a+b | B. | 2b-a | C. | 3b-a | D. | 以上都不对 |
12.已知一次函数y=kx+b与直线y=3x-2平行,与直线y=2x+3相交于y轴上一点,则k、b的值分别为( )
| A. | k=3,b=2 | B. | k=3,b=3 | C. | k=-2,b=3 | D. | k=2,b=3 |
 在一节数学课上,老师布置了一个任务:
在一节数学课上,老师布置了一个任务: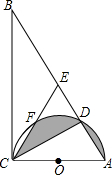 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=12,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,求图中阴影部分的面积.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=12,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,求图中阴影部分的面积.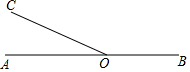 在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程)
在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程)