题目内容
8.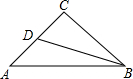 如图,在△ABC中,∠C=90°,AC=BC,AB=4,BD是角平分线,则BC+CD=4.
如图,在△ABC中,∠C=90°,AC=BC,AB=4,BD是角平分线,则BC+CD=4.
分析 过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用“HL”证明Rt△BCD和Rt△BED全等,根据全等三角形对应边相等可得BC=BE,再求出△ADE是等腰直角三角形,然后求出AE=DE,最后等量代换可得BC+CD=AB.
解答 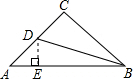 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,BD是角平分线,
∴DE=CD,
在Rt△BCD和Rt△BED中,$\left\{\begin{array}{l}{BD=BD}\\{CD=DE}\end{array}\right.$,
∴Rt△BCD≌Rt△BED(HL),
∴BC=BE,
∵∠C=90°,AC=BC,
∴∠A=45°,
∴△ADE是等腰直角三角形,
∴AE=DE,
∵BE+AE=AB,
∴BC+CD=AB,
∵AB=4,
∴BC+CD=4.
故答案为:4.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
16. 如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
 如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )
如图,已知点P的坐标为(12,5),则点P到原点O的距离为( )| A. | 5 | B. | 12 | C. | 13 | D. | 17 |
3. 已知一次函数的表达式为y=2x+4.
已知一次函数的表达式为y=2x+4.
(1)填表,用表格表示变量y与x的一次函数关系.
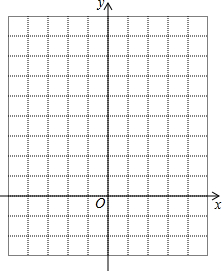
(2)在如图的平面直角坐标系中画出该函数的图象.
 已知一次函数的表达式为y=2x+4.
已知一次函数的表达式为y=2x+4.(1)填表,用表格表示变量y与x的一次函数关系.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| Y | … | 8 | … |
13.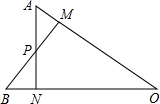 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )| A. | OA=OB | B. | AM=BN | ||
| C. | 点P在∠AOB的平分线上 | D. | AM=PM |
17.方程x2-3x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
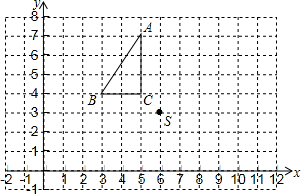 △ABC和点S在平面直角坐标系中的位置如图所示.
△ABC和点S在平面直角坐标系中的位置如图所示. 如图,梯形ABCD中,AD∥BC,∠DAE=∠C,AD=5,若此梯形的周长是29,则△ABE的周长是19.
如图,梯形ABCD中,AD∥BC,∠DAE=∠C,AD=5,若此梯形的周长是29,则△ABE的周长是19.