题目内容
13.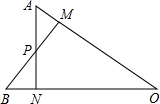 如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )
如图,AN⊥OB,BM⊥OA,垂足分别是N、M,BM与AN交于点P,若OM=ON,则下列结论不正确的是( )| A. | OA=OB | B. | AM=BN | ||
| C. | 点P在∠AOB的平分线上 | D. | AM=PM |
分析 连接OP,证明△OPM与△OPN全等,再利用全等三角形的性质和角平分线的性质解答即可.
解答 解:连接OP,∵AN⊥OB,BM⊥OA,
∴在Rt△OPM与Rt△OPN中
$\left\{\begin{array}{l}{ON=OM}\\{OP=OP}\end{array}\right.$,
∴Rt△OPM≌Rt△OPN(HL),
∴∠PON=∠POM,PN=PM,
∴点P在∠AOB的平分线上,故C正确,
在△APM与△PBN中
$\left\{\begin{array}{l}{∠PNB=∠PMA=90°}\\{PN=PM}\\{∠BPN=∠APM}\end{array}\right.$,
∴△APM≌△PBN(ASA),
∴BN=AM,故B正确;
∴OA=AM+OM,OB=BN+ON,
即OA=OB,故A正确;
故选D
点评 此题考查全等三角形的判定和性质,关键是证明△OPM与△OPN全等.

练习册系列答案
相关题目
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④∠BDC=∠BAC.其中正确的结论有( )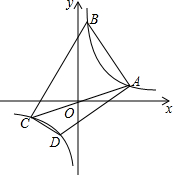 如图,在平面直角坐标中,四边形ABCD的四个顶点都在双曲线y=$\frac{1}{x}$上,其中,点A、B在第一象限,点C、D在第三象限,对角线AC经过原点O,求证:∠BAD=∠BCD.
如图,在平面直角坐标中,四边形ABCD的四个顶点都在双曲线y=$\frac{1}{x}$上,其中,点A、B在第一象限,点C、D在第三象限,对角线AC经过原点O,求证:∠BAD=∠BCD.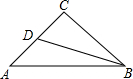 如图,在△ABC中,∠C=90°,AC=BC,AB=4,BD是角平分线,则BC+CD=4.
如图,在△ABC中,∠C=90°,AC=BC,AB=4,BD是角平分线,则BC+CD=4.