题目内容
13.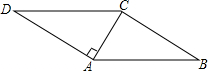 在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )
在?ABCD中,AC⊥AD,∠B=30°,AC=2,则?ABCD的周长是( )| A. | 4+2$\sqrt{3}$ | B. | 8 | C. | 8+4$\sqrt{3}$ | D. | 16 |
分析 由AC⊥AD,∠B=30°,AC=2,根据含30°角的直角三角形的性质,可求得AB的长,然后由勾股定理求得BC的长,继而求得答案.
解答 解:∵AC⊥AD,∠B=30°,AC=2,
∴AB=2AC=4,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$,
∴?ABCD的周长是:2(AB+BC)=8+4$\sqrt{3}$.
故选C.
点评 此题考查了平行四边形的性质、含30°角的直角三角形的性质以及勾股定理.注意平行四边形的对边相等.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.$\frac{3}{2}$的相反数是( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
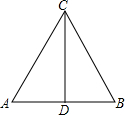 已知:如图,等边△ABC的边长是6cm.
已知:如图,等边△ABC的边长是6cm.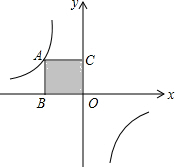 如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.
如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.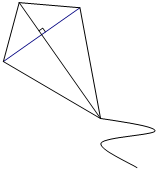 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?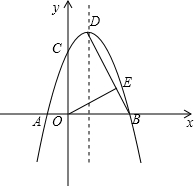 如图,抛物线y=-x2+bx+c与x轴交于A、B点,与y轴交于C点,顶点为D,其中点A、C的坐标分别是(-1,0)、(0,3).
如图,抛物线y=-x2+bx+c与x轴交于A、B点,与y轴交于C点,顶点为D,其中点A、C的坐标分别是(-1,0)、(0,3).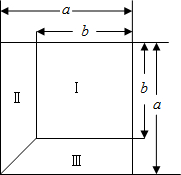 根据图示,回答下列问题
根据图示,回答下列问题