题目内容
14．
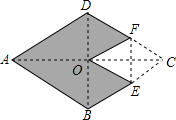如图，菱形ABCD中，AC与BD相交于点O．将菱形沿EF折叠，使点C与点O重合．若AC=8，BD=6，则图中阴影部分的面积为18．
分析 根据菱形的对角线互相平分求出OC，再根据翻折的定义判断出EF是△BCD的中位线，然后根据三角形的中位线平行于第三边并且等于第三边的一半求出EF，最后根据阴影部分的面积等于两个菱形的面积的差列式计算即可得解．
解答 解：在菱形ABCD中，OC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4，
∵将菱形沿EF折叠，使点C与点O重合，
∴EF是△BCD的中位线，
∴EF=$\frac{1}{2}$BD=$\frac{1}{2}$×6=3，
∴阴影部分的面积=$\frac{1}{2}$×8×6-$\frac{1}{2}$×4×3=24-6=18．
故答案为：18．
点评 本题考查了菱形的性质，三角形的中位线平行于第三边并且等于第三边的一半，要注意菱形的面积等于对角线乘积的一半的应用．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
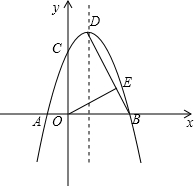如图，抛物线y=-x2+bx+c与x轴交于A、B点，与y轴交于C点，顶点为D，其中点A、C的坐标分别是（-1，0）、（0，3）．
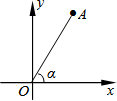如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα=$\frac{3}{2}$，则t的值是$\frac{9}{2}$．
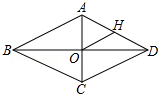如图，菱形ABCD中，对角线AC、BC相交于点O，H为AD边中点，菱形ABCD的周长为28，求OH的长？
根据图示，回答下列问题