题目内容
19.一个两位数,它的十位数字比个位数字小4,若把两个数字位置调换,所得的两位数与原两位数的乘积等于765,则原两位数是?分析 设十位数字为x,则个位数字为(x+4),这个两位数可表示为:10x+(x+4)=11x+4,对调后的两位数十位数字为(x+4),个位数字为x,所得两位数可表示为:10(x+4)+x=11x+40,为根据题意列出方程,求出x的值,两位数即可求出.
解答 解:设十位数字为x,则个位数字为(x+4),这个两位数可表示为:10x+(x+4)=11x+4,对调后的两位数十位数字为(x+4),个位数字为x,所得两位数可表示为:10(x+4)+x=11x+40,由题意可得:
(11x+4)(11x+40)=765,
解得x1=1,x2=-5(舍去).
x+4=1+4=5.
答:这个两位数为15.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
1.已知点P(a,a+3)在抛物线y=x2-7x+19图象上,则点P关于原点O的对称点P′的坐标是( )
| A. | (4,7) | B. | (-4,-7) | C. | (4,-7) | D. | (-4,7) |
14.下列各组数中,相等的是( )
| A. | -1与(-4)+(-3) | B. | 3与-(-3) | C. | $\frac{3^2}{4}$与$\frac{9}{16}$ | D. | |-16|与-16 |
4.在${({-\sqrt{2}})^2}$,$\root{3}{8}$,0,$\sqrt{9}$,0.010010001…,π,$\frac{22}{7}$,-0.333…,$\sqrt{5}$,3.1415,2.010101…(相邻两个1之间有1个0)中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.“a<b”的反面是( )
| A. | a≠b | B. | a>b | C. | a=b | D. | a≥b |
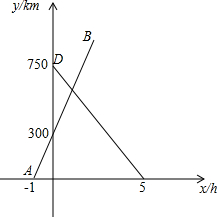 铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).
铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).