题目内容
12.当m为何取值范围时,方程$\frac{2}{x}$-$\frac{xm}{{x}^{2}-x}$=1+$\frac{1}{x-1}$无实数解.分析 分式方程去分母转化为整式方程,根据分式方程无解得到最简公分母为0,求出x的值,代入整式方程即可求出m的值,还要注意整式方程无解的情形.
解答 解:方程两边同时乘以x(x-1)得:
2(x-1)-mx=x2-x+x
去括号得:
2x-mx-2=x2,即x2+(m-2)x+2=0,
∵分式方程无实数解,
∴x=0或x=1,
把x=0代入x2+(m-2)x+2=0,不存在m的值;
把x=1代入x2+(m-2)x+2=0,
解得:m=-1.
当整式方程x2+(m-2)x+2=0中,△=(m-2)2-8<0时,该方程无解,
∴2-2$\sqrt{2}$<m<2+2$\sqrt{2}$,
即当2-2$\sqrt{2}$<m<2+2$\sqrt{2}$时,原方程无解,
综上所述,当2-2$\sqrt{2}$<m<2+2$\sqrt{2}$或m=-1时,方程$\frac{2}{x}$-$\frac{xm}{{x}^{2}-x}$=1+$\frac{1}{x-1}$无实数解.
点评 此题考查了分式方程的解,解决本题的关键是明确分式方程无解的条件为最简公分母为0或所得的整式方程无解.在解方程的过程中因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根,增根是令分母等于0的值,不是原分式方程的解.

练习册系列答案
相关题目
7.学校体育室有两个球筐,已知甲筐内的球比乙筐内球的个数的2倍还多4只. 现进行如下操作:第一次,从甲筐中取一只球放入乙筐;第二次,又从甲筐取出若干球放入乙筐,这次取出的球的个数是第一次移动后乙筐内球的个数的两倍.
若设乙球筐内原来有a只球
(1)请你填写下表(用含a的代数式表示)
(2)根据以上表格,化简后可知甲球筐内最后还剩下1个球.
(3)若最后乙球筐内有球27只,请求a的值.
若设乙球筐内原来有a只球
(1)请你填写下表(用含a的代数式表示)
| 甲球筐内球的个数 | 乙球筐内球的个数 | |
| 原来: | 2a+4 | a |
| 第一次后: | 2a+3 | a+1 |
| 第二次后: | 11 | 3a+3 |
(3)若最后乙球筐内有球27只,请求a的值.
4.三棱柱的截面不可能是( )
| A. | 三角形 | B. | 长方形 | C. | 五边形 | D. | 六边形 |
 图中,AB=AC及AP平分∠BAC.AP是否为△ABC的一条垂直平分线?试解释你的答案.
图中,AB=AC及AP平分∠BAC.AP是否为△ABC的一条垂直平分线?试解释你的答案.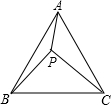 P是等边三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长度.
P是等边三角形ABC内一点,PA=2,PB=2$\sqrt{3}$,PC=4,求BC的长度.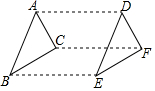 如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE,②AD=BE,③∠ACB=∠DFE,④BC=DE,其中正确的有3个.
如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE,②AD=BE,③∠ACB=∠DFE,④BC=DE,其中正确的有3个.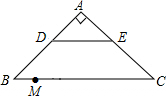 如图,在等腰直角三角形ABC中,AB=AC,斜边BC=20,点D,E分别是AB,AC的中点,M是BC上一点,BM=3,点N是线段MC上的一个动点,DN与ME相交于点O,若△OMN是直角三角形,则MN的长是2或$\frac{49}{12}$.
如图,在等腰直角三角形ABC中,AB=AC,斜边BC=20,点D,E分别是AB,AC的中点,M是BC上一点,BM=3,点N是线段MC上的一个动点,DN与ME相交于点O,若△OMN是直角三角形,则MN的长是2或$\frac{49}{12}$.